Question

已知直平行六面体ABCD—A₁B₁C₁D₁的各条棱长均为3，∠BAD＝60°，长为2的线段MN的一个端点M在DD₁上运动，另一端点N在底面ABCD上运动，则MN的中点P的轨迹（曲面）与共一顶点D的三个面所围成的几何体的体积为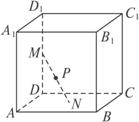

A.                B.                 C.               D.

Answer 1

A 

解析：∵△MDN为直角三角形，P为MN的中点，∴DP=MN=1.∴P点的轨迹是以D为球心半径为1的球被平行六面体截得的曲面，由题意得∠ADC=120°=，∴它的体积是该球体积的×=，即××1³=.