摘要：解:(Ⅰ)作A1D⊥AC.垂足为D.由面A1ACC1⊥面ABC.得A1D⊥面ABC∴∠A1AD为A1A与面ABC所成的角.∵AA1⊥A1C.AA1＝A1C.∴∠A1AD＝45°为所求.(Ⅱ)作DE⊥AB.垂足为E.连A1E.则由A1D⊥面ABC.得A1E⊥AB.∴∠A1ED是面A1ABB1与面ABC所成二面角的平面角.由已知.AB⊥BC.得ED∥BC.
网址：http://m.1010jiajiao.com/timu_id_425241[举报]
如图，在锐角△ABC中，AB<AC，AD是边BC上的高，P是线段AD内一点。过P作PE⊥AC，垂足为E，做PF⊥AB，垂足为F。O1、O2分别是△BDF、△CDE的外心。求证：O1、O2、E、F四点共圆的充要条件为P是△ABC的垂心。
如图，在锐角△ABC中，AB<AC，AD是边BC上的高，P是线段AD内一点。过P作PE⊥AC，垂足为E，做PF⊥AB，垂足为F。O1、O2分别是△BDF、△CDE的外心。求证：O1、O2、E、F四点共圆的充要条件为P是△ABC的垂心。
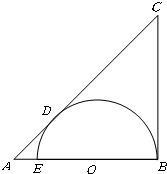如图：EB是⊙O的直径，A是BE的延长线上一点，过A作⊙O的切线AC，切点为D，过B作⊙O的切线BC，交AC于点C，若EB=BC=6，求：AD，AE的长．
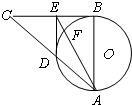如图：在Rt∠ABC中，AB=BC，以AB为直径的⊙O交AC于点D，过D作DE⊥BC，垂足为E，连接AE交⊙O于点F，求证：BE•CE=EF•EA．