题目内容
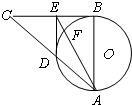 如图:在Rt∠ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:BE•CE=EF•EA.
如图:在Rt∠ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:BE•CE=EF•EA.
分析:欲证明BE•CE=EF•EA.在圆中线段利用由切割线定理得EB2=EF•FA,进而利用四边形BODE中的线段,证得BE=CE即可.
解答: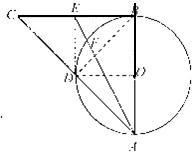 证明:因为Rt△ABC中,∠ABC=90°
证明:因为Rt△ABC中,∠ABC=90°
所以OB⊥CB
所以CB为⊙O的切线(2分)
所以EB2=EF•FA(5分)
连接OD,因为AB=BC
所以∠BAC=45°
所以∠BOD=90°
在四边形BODE中,∠BOD=∠OBE=∠BED=90°
所以BODE为矩形(7分)
所以BE=OD=OB=
AB=
BC.
即BE=CE.
所以BE•CE=EF•EA.(10分)
 证明:因为Rt△ABC中,∠ABC=90°
证明:因为Rt△ABC中,∠ABC=90°所以OB⊥CB
所以CB为⊙O的切线(2分)
所以EB2=EF•FA(5分)
连接OD,因为AB=BC
所以∠BAC=45°
所以∠BOD=90°
在四边形BODE中,∠BOD=∠OBE=∠BED=90°
所以BODE为矩形(7分)
所以BE=OD=OB=
| 1 |
| 2 |
| 1 |
| 2 |
即BE=CE.
所以BE•CE=EF•EA.(10分)
点评:此题考查的是直角三角形的性质、勾股定理的应用、与圆有关的比例线段以及切割线定理,属于基础题.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=