题目内容
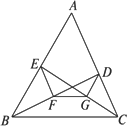
如图,在锐角△ABC中,AB<AC,AD是边BC上的高,P是线段AD内一点。过P作PE⊥AC,垂足为E,做PF⊥AB,垂足为F。O1、O2分别是△BDF、△CDE的外心。求证:O1、O2、E、F四点共圆的充要条件为P是△ABC的垂心。

证明略
解析:
证明:连结BP、CP、O1O2、EO2、EF、FO1。因为PD⊥BC,PF⊥AB,故B、D、P、F四点共圆,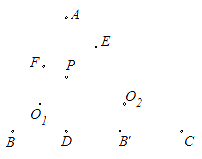
且BP为该圆的直径。又因为O1是△BDF的外心,故O1在BP上且是BP的中点。同理可证C、D、P、E四点共圆,且O2是的CP中点。综合以上知O1O2∥BC,所以∠PO2O1=∠PCB。因为AF·AB=AP·AD=AE·AC,所以B、C、E、F四点共圆。
充分性:设P是△ABC的垂心,由于PE⊥AC,PF⊥AB,所以B、O1、P、E四点共线,C、O2、P、F四点共线,∠FO2O1=∠FCB=∠FEB=∠FEO1,故O1、O2、E、F四点共圆。
必要性:设O1、O2、E、F四点共圆,故∠O1O2E+∠EFO1=180°。
由于∠PO2O1=∠PCB=∠ACB??∠ACP,又因为O2是直角△CEP的斜边中点,也就是△CEP的外心,所以∠PO2E=2∠ACP。因为O1是直角△BFP的斜边中点,也就是△BFP的外心,从而∠PFO1=90°??∠BFO1=90°??∠ABP。因为B、C、E、F四点共圆,所以∠AFE=∠ACB,∠PFE=90°??∠ACB。于是,由∠O1O2E+∠EFO1=180°得
(∠ACB??∠ACP)+2∠ACP+(90°??∠ABP)+(90°??∠ACB)=180°,即∠ABP=∠ACP。又因为AB<AC,AD⊥BC,故BD<CD。设B'是点B关于直线AD的对称点,则B'在线段DC上且B'D=BD。连结AB'、PB'。由对称性,有∠AB'P=∠ABP,从而∠AB'P=∠ACP,所以A、P、B'、C四点共圆。由此可知∠PB'B=∠CAP=90°??∠ACB。因为∠PBC=∠PB'B,
故∠PBC+∠ACB=(90°??∠ACB)+∠ACB=90°,故直线BP和AC垂直。由题设P在边BC的高上,所以P是△ABC的垂心。

 中考解读考点精练系列答案
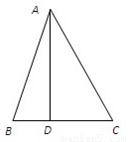
中考解读考点精练系列答案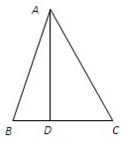 如图,在锐角△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6,则∠BAC的大小为
如图,在锐角△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6,则∠BAC的大小为