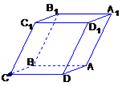
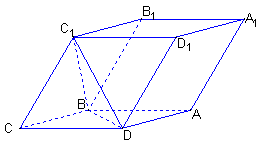
摘要:又C1C平面AC1.∴C1C⊥BD.知AC⊥BD.C1O⊥BD.∴∠C1OC是二面角α―BD―β的平面角.
网址:http://m.1010jiajiao.com/timu_id_425205[举报]
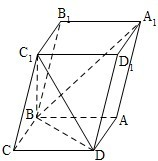
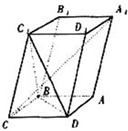 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD上菱形,且∠C1CB=∠C1CD=∠BCD,
如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD上菱形,且∠C1CB=∠C1CD=∠BCD,(1)证明:C1C⊥BD;
(2)当
| CD | CC1 |
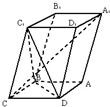 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°.
如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°.(1)证明:C1C⊥BD;
(2)假定CD=2,CC1=
| 3 |
| 2 |
(3)当
| CD |
| CC1 |
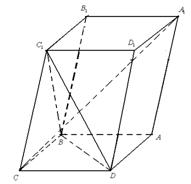
如图,已知斜四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.
(1) 证明:C1C⊥BD;
(2) 当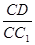 的值为多少时,能使A1C⊥平面C1BD?请给出证明
的值为多少时,能使A1C⊥平面C1BD?请给出证明
查看习题详情和答案>>