题目内容
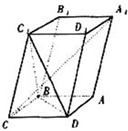 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD上菱形,且∠C1CB=∠C1CD=∠BCD,
如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD上菱形,且∠C1CB=∠C1CD=∠BCD,(1)证明:C1C⊥BD;
(2)当
| CD | CC1 |
分析:(1)连接A1C1、AC和BD交于O,连接C1O.证明BD垂直平面平面AC1内的两条相交直线AC,C1O,即可证明C1C⊥BD;
(2)当
=1时,能使A1C⊥平面C1BD,A1C与C1O相交于G,说明点G是正三角形C1BD的中心,证明CG⊥平面C1BD,即可证明A1C⊥平面C1BD.
(2)当
| CD |
| CC1 |
解答:(1)证明:如图,连接A1C1、AC和BD交于O,连接C1O.
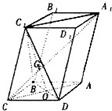
∵四边形ABCD是菱形,
∴AC⊥BD,BC=CD.
又∵∠BCC1=∠DCC1,C1C=C1C,
∴△C1BC≌△C1DC,
∴C1B=C1D,
∵DO=OB
∴C1O⊥BD,(3分)
但AC⊥BD,AC∩C1O=O,
∴BD⊥平面AC1,
又C1C?平面AC1,
∴C1C⊥BD.(6分)
(2)当
=1时,能使A1C⊥平面C1BD.
∵
=1,
∴BC=CD=C1C,
又∠BCD=∠C1CB=∠C1CD,
由此可推得BD=C1B=C1D.
∴三棱锥C-C1BD是正三棱锥.(9分)
设A1C与C1O相交于G.
∵A1C1∥AC,且A1C1:OC=2:1,
∴C1G:GO=2:1.
又C1O是正三角形C1BD的BD边上的高和中线,
∴点G是正三角形C1BD的中心,
∴CG⊥平面C1BD,
即A1C⊥平面C1BD.(12分)

∵四边形ABCD是菱形,
∴AC⊥BD,BC=CD.
又∵∠BCC1=∠DCC1,C1C=C1C,
∴△C1BC≌△C1DC,
∴C1B=C1D,
∵DO=OB
∴C1O⊥BD,(3分)
但AC⊥BD,AC∩C1O=O,
∴BD⊥平面AC1,
又C1C?平面AC1,
∴C1C⊥BD.(6分)
(2)当
| CD |
| CC1 |
∵
| CD |
| CC1 |
∴BC=CD=C1C,
又∠BCD=∠C1CB=∠C1CD,
由此可推得BD=C1B=C1D.
∴三棱锥C-C1BD是正三棱锥.(9分)
设A1C与C1O相交于G.
∵A1C1∥AC,且A1C1:OC=2:1,
∴C1G:GO=2:1.
又C1O是正三角形C1BD的BD边上的高和中线,
∴点G是正三角形C1BD的中心,
∴CG⊥平面C1BD,
即A1C⊥平面C1BD.(12分)
点评:本小题主要考查直线与直线、直线与平面的关系,逻辑推理能力,考查空间想象能力,是中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)
如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱) 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.