题目内容
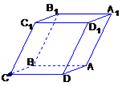
如图,已知平行六面体ABCD—A1B1C1D1的底面?ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.
(1)求证: C1C⊥BD![]()
(2)当![]() 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
(1)证明略,(2) ![]() =1时,A1C⊥平面C1BD.
=1时,A1C⊥平面C1BD.
解析:
(1)证明: 设![]() =
=![]() ,
, ![]() =
=![]() ,
,![]() ,依题意,|
,依题意,|![]() |=|
|=|![]() |,
|,![]() 、
、![]() 、?
、?![]() 中两两所成夹角为θ,于是
中两两所成夹角为θ,于是
![]() =
=![]() -
-![]() ,
,
![]() =
=![]() (
(![]() -
-![]() )=
)=![]() ·
·![]() -
-![]() ·
·![]() =|
=|![]() |·|
|·|![]() |cosθ-|
|cosθ-|![]() |·|
|·|![]() |cosθ=0,∴C1C⊥BD.
|cosθ=0,∴C1C⊥BD.
(2)解:若使A1C⊥平面C1BD,只须证A1C⊥BD,A1C⊥DC1,
由![]()
=(![]() +
+![]() +
+![]() )·(
)·(![]() -
-![]() )=|
)=|![]() |2+
|2+![]() ·
·![]() -
-![]() ·
·![]() -|
-|![]() |2
|2
=|![]() |2-|
|2-|![]() |2+|
|2+|![]() |·|
|·|![]() |cosθ-|
|cosθ-|![]() |·|
|·|![]() |·cosθ=0,得
|·cosθ=0,得
当|![]() =|
=|![]() |时,A1C⊥DC1,同理可证当|
|时,A1C⊥DC1,同理可证当|![]() |=|
|=|![]() |时,A1C⊥BD,
|时,A1C⊥BD,
∴![]() =1时,A1C⊥平面C1BD.
=1时,A1C⊥平面C1BD.

练习册系列答案
相关题目
 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)
如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱) 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.