题目内容
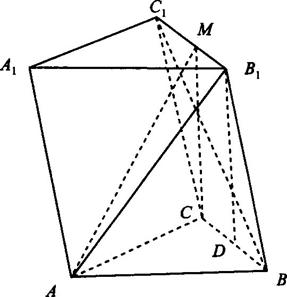
如图,已知斜四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.
(1) 证明:C1C⊥BD;
(2) 当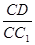 的值为多少时,能使A1C⊥平面C1BD?请给出证明
的值为多少时,能使A1C⊥平面C1BD?请给出证明
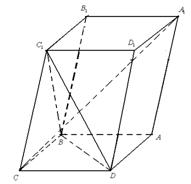
(1)证明:连结A1C1、AC,AC和BD交于O,连结C1O.
∵ 四边形ABCD是菱形,
∴ AC⊥BD,BC=CD.
又∵ ∠BCC1=∠DCC1,C1C=C1C,
∴ △C1BC≌△C1DC,
∴ C1B=C1D,
∵ DO=OB,
∴ C1O⊥BD, ——3分
但AC⊥BD,AC∩C1O= O,
∴ BD⊥平面AC1.
又 C1C 平面AC1,
平面AC1,
∴ C1C⊥BD. ——6分
(2) 当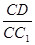 =1时,能使A1C⊥平面C1BD.
=1时,能使A1C⊥平面C1BD.
证明一:
∵ 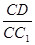 =1,
=1,
∴ BC=CD=C1C,
又∠BCD=∠C1CB=∠C1CD,
由此可推得BD=C1B=C1D.
∴ 三棱锥C-C1BD是正三棱锥. ——9分
设A1C与C1O相交于G.
∵ A1C1∥AC,且A1C1:OC=2:1,
∴ C1G︰GO=2︰1.
又C1O是正三角形C1BD的BD边上的高和中线,
∴ 点G是正三角形C1BD的中心,
∴ CG⊥平面C1BD.
即A1C⊥平面C1BD. ——12分
证明二:
由(Ⅰ)知,BD⊥平面AC1,
∵ A1C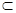 平面AC1,
平面AC1,
∴ BD⊥A1C. ——9分
当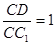 时,斜四棱柱的六个面是全等的菱形,
时,斜四棱柱的六个面是全等的菱形,
同BD⊥A1C的证法可得BC1⊥A1C.
BD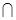 BC1=B,
BC1=B,
∴ A1C⊥平面C1BD.
【解析】略

 53天天练系列答案
53天天练系列答案 的底面是直角三角形,AC⊥CB,∠ABC=
的底面是直角三角形,AC⊥CB,∠ABC=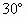 ,侧面
,侧面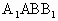 是边长为a的菱形,且垂直于底面,
是边长为a的菱形,且垂直于底面,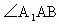 =
=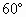 ,E、F分别是
,E、F分别是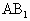 、BC的中点.
、BC的中点.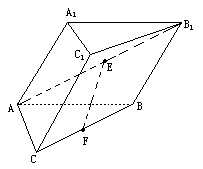
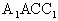 ;
;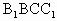 的体积;
的体积;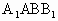 所成角的正切值.
所成角的正切值.