(Ⅰ)证明:连结OF.CE.A′O.如图9―73∵AE＝BF ∴EB＝CF OC＝CB ∠OCF＝∠CBE∴△OCF≌△CEB ∴∠ECB＝∠FOC.∴OF⊥CE又∵CC′⊥平面AC CE⊥OF ∴C——青夏教育精英家教网——

摘要：(Ⅰ)证明:连结OF.CE.A′O.如图9―73∵AE＝BF ∴EB＝CF OC＝CB ∠OCF＝∠CBE∴△OCF≌△CEB ∴∠ECB＝∠FOC.∴OF⊥CE又∵CC′⊥平面AC CE⊥OF ∴C′E⊥OF又∵EB⊥平面BC′.C′B⊥B′C ∴C′E⊥B′C又∵A′O∥B′C ∴C′E⊥A′O又∵A′O∩OF＝O C′E⊥A′O C′E⊥OF

网址：http://m.1010jiajiao.com/timu_id_425175[举报]

(几何证明选讲选做题)已知：如图，在△ABC中，∠ABC＝90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，连结DB、DE、OC。若AD＝2，AE＝1，则CD的长为。

查看习题详情和答案>>

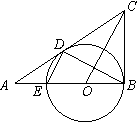
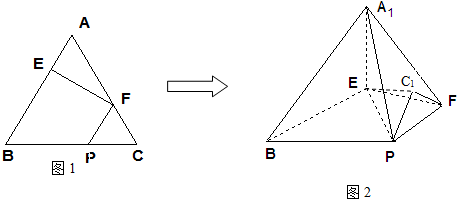
在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE：EB=CF：FA=CP：PB=1：2（如图1）．将△AEF、△CFP分别沿EF、PF折起到△A₁EF和△C₁FP的位置，使二面角A₁-EF-B和C₁-PF-B均成直二面角，连结A₁B、A₁P、EC₁（如图2）
（1）求证：A₁E⊥平面BEP；
（2）设正△ABC的边长为3，以

为正交基底，建立空间直角坐标系．
①求点C₁的坐标；
②直线EC₁与平面C₁PF所成角的大小；
③求二面角B-A₁P-F的余弦值．

查看习题详情和答案>>

在△ABC中，a，b，c分别为内角A，B，C所对的边，且满足

．
（1）证明：b+c=2a；
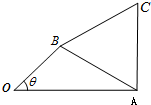
（2）如图，点O是△ABC外一点，设∠AOB=θ（0＜θ＜π），OA=2OB=2，当b=c时，求平面四边形OACB面积的最大值．

查看习题详情和答案>>

（本题为选做题，请在下列三题中任选一题作答）
A（《几何证明选讲》选做题）．如图：直角三角形ABC中，∠B=90°，AB=4，以BC为直径的圆交边AC于点D，AD=2，则∠C的大小为

．
B（《坐标系与参数方程选讲》选做题）．已知直线的极坐标方程为ρsin(θ+

，则点A（2，

）到这条直线的距离为

．
C（不等式选讲）不等式|x-1|+|x|＜3的解集是

查看习题详情和答案>>

在A，B，C，D四小题中只能选做2题，每题10分，共计20分．
A、如图，AB为⊙O的直径，BC切⊙O于B，AC交⊙O于P，CE=BE，E在BC上．求证：PE是⊙O的切线．
B、设M是把坐标平面上的点的横坐标伸长到2倍，纵坐标伸长到3倍的伸压变换．
（1）求矩阵M的特征值及相应的特征向量；
（2）求逆矩阵M^-1以及椭圆

=1在M^-1的作用下的新曲线的方程．
C、已知某圆的极坐标方程为：ρ2-4

)+6=0．
（Ⅰ）将极坐标方程化为普通方程；并选择恰当的参数写出它的参数方程；
（Ⅱ）若点P（x，y）在该圆上，求x+y的最大值和最小值．
D、若关于x的不等式|x+2|+|x-1|≥a的解集为R，求实数a的取值范围．查看习题详情和答案>>