题目内容
 在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足
在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足| sinB+sinC |
| sinA |
| 2-cosB-cosC |
| cosA |
(1)证明:b+c=2a;
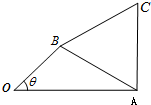
(2)如图,点O是△ABC外一点,设∠AOB=θ(0<θ<π),OA=2OB=2,当b=c时,求平面四边形OACB面积的最大值.
分析:(1)由已知条件化简可得sinC+sinB=2sinA,再由正弦定理可得b+c=2a;
(2)由条件和(1)的结论可得△ABC为等边三角形,利用S△OACB=S△OAB+S△OBC=
OA•OB•sinθ+
AB2,结合辅助角公式,可得平面四边形OACB面积的最大值.
(2)由条件和(1)的结论可得△ABC为等边三角形,利用S△OACB=S△OAB+S△OBC=
| 1 |
| 2 |
| ||
| 4 |
解答:(1)证明:∵
=
,
∴sinBcosA+sinCcosA=2sinA-cosBsinA-cosCsinA,
∴sinBcosA+cosBsinA+sinCcosA+cosCsinA=2sinA,
∴sin(A+B)+sin(A+C)=2sinA,
∴sinC+sinB=2sinA,
∴b+c=2a;
(2)解:∵b+c=2a,b=c,
∴a=b=c,∴△ABC为等边三角形,
∴S△OACB=S△OAB+S△OBC=
OA•OB•sinθ+
AB2=sinθ+
(OA2+OB2-2OA•OB•cosθ)
=sinθ-
cosθ+
=2sin(θ-
)+
.
∵0<θ<π,
∴-
<θ-
<
,
当且仅当θ-
=
,即θ=
时取最大值,最大值为2+
.
| sinB+sinC |
| sinA |
| 2-cosB-cosC |
| cosA |
∴sinBcosA+sinCcosA=2sinA-cosBsinA-cosCsinA,
∴sinBcosA+cosBsinA+sinCcosA+cosCsinA=2sinA,
∴sin(A+B)+sin(A+C)=2sinA,
∴sinC+sinB=2sinA,
∴b+c=2a;
(2)解:∵b+c=2a,b=c,
∴a=b=c,∴△ABC为等边三角形,
∴S△OACB=S△OAB+S△OBC=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
=sinθ-
| 3 |
5
| ||
| 4 |
| π |
| 3 |
5
| ||
| 4 |
∵0<θ<π,
∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
当且仅当θ-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
5
| ||
| 4 |
点评:本题考查两角和与差的三角函数公式,涉及余弦定理和三角形的面积,考查三角函数的性质,正确表示平面四边形OACB面积是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|