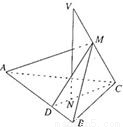
摘要:(Ⅱ)证明:∵VC平面VCN.∴AB⊥VC又∵在△VCN和△CDM中.∠CVN=∠MDC.∠VCN=∠VCN ∴∠DMC=∠VNC=90°.∴DM⊥VC
网址:http://m.1010jiajiao.com/timu_id_425172[举报]
已知VC是△ABC所在平面的一条斜线,点N是V在平面ABC上的射影,且在△ABC的高CD上(如图).
(1)证明:∠MDC是二面角M-AB-C的平面角;
(2)当∠MDC=∠CVN时,证明:VC⊥平面AMB;
查看习题详情和答案>>
已知VC是△ABC所在平面的一条斜线,点N是V在平面ABC上的射影,且在△ABC的高CD上(如图).
(1)证明:∠MDC是二面角M-AB-C的平面角;
(2)当∠MDC=∠CVN时,证明:VC⊥平面AMB;
查看习题详情和答案>> 甲.如图1,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB:AD=
甲.如图1,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB:AD=| 2 |
(1)求VC与平面ABCD所成的角;
(2)求二面角V-FC-B的度数;
(3)当V到平面ABCD的距离是3时,求B到平面VFC的距离.
乙、如图正方体ABCD-A1B1C1D1中,E、F、G分别是B1B、AB、BC的中点.
(1)证明:D1F⊥EG;
(2)证明:D1F⊥平面AEG;
(3)求cos<
| AE |
| D1B |
注意:考生在(19甲)、(19乙)两题中选一题作答,如果两题都答,只以(19甲)计分.
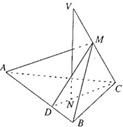 19、如图已知VC是△ABC所在平面的一条斜线,点N是V在平面ABC上的射影,且在△ABC的高CD上.AB=a,VC与AB之间的距离为h,点M∈VC.
19、如图已知VC是△ABC所在平面的一条斜线,点N是V在平面ABC上的射影,且在△ABC的高CD上.AB=a,VC与AB之间的距离为h,点M∈VC.