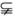题目内容
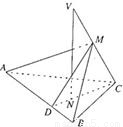
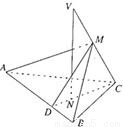
如图已知VC是△ABC所在平面的一条斜线，点N是V在平面ABC上的射影，且在△ABC的高CD上．AB=a，VC与AB之间的距离为h，点M∈VC．（1）证明∠MDC是二面角M-AB-C的平面角；
（2）当∠MDC=∠CVN时，证明VC⊥平面AMB．
【答案】分析：（1）直接利用二面角平面角的定义进行证明∠MDC为二面角M-AB-C的平面角；
（2）欲证VC⊥平面AMB，根据直线与平面垂直的判定定理可知只需证VC与平面AMB内两相交直线垂直，易证DM⊥VC，AB⊥VC，问题得证．
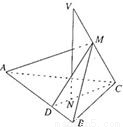
解答：（1）证明：如图由已知，
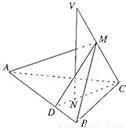
CD⊥AB，VN⊥平面ABC，N∈CD，AB?平面ABC，
∴VN⊥AB．
∴AB⊥平面VNC．
又V、M、N、D都在VNC所在的平面内，
所以，DM与VN必相交，且AB⊥DM，AB⊥CD，
∴∠MDC为二面角M-AB-C的平面角．
（2）证明：由已知，∠MDC=∠CVN，
在△VNC与△DMC中，
∠NCV=∠MCD，
又∵∠VNC=90°，
∴∠DMC=∠VNC=90°，
故有DM⊥VC，又AB⊥VC，
∴VC⊥平面AMB．
点评：本小题主要考查线面关系的基本概念，考查运用直线与直线、直线与平面的基本性质进行计算和证明的能力．
（2）欲证VC⊥平面AMB，根据直线与平面垂直的判定定理可知只需证VC与平面AMB内两相交直线垂直，易证DM⊥VC，AB⊥VC，问题得证．
解答：（1）证明：如图由已知，
CD⊥AB，VN⊥平面ABC，N∈CD，AB?平面ABC，
∴VN⊥AB．
∴AB⊥平面VNC．
又V、M、N、D都在VNC所在的平面内，
所以，DM与VN必相交，且AB⊥DM，AB⊥CD，
∴∠MDC为二面角M-AB-C的平面角．
（2）证明：由已知，∠MDC=∠CVN，
在△VNC与△DMC中，
∠NCV=∠MCD，
又∵∠VNC=90°，
∴∠DMC=∠VNC=90°，
故有DM⊥VC，又AB⊥VC，
∴VC⊥平面AMB．
点评：本小题主要考查线面关系的基本概念，考查运用直线与直线、直线与平面的基本性质进行计算和证明的能力．
练习册系列答案
相关题目
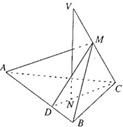19、如图已知VC是△ABC所在平面的一条斜线，点N是V在平面ABC上的射影，且在△ABC的高CD上．AB=a，VC与AB之间的距离为h，点M∈VC．
