题目内容
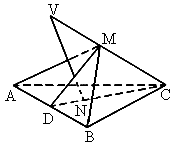
已知VC是△ABC所在平面的一条斜线，点N是V在平面ABC上的射影，且在△ABC的高CD上(如图).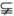
(1)证明：∠MDC是二面角M-AB-C的平面角；
(2)当∠MDC=∠CVN时，证明：VC⊥平面AMB；
证明：(1)由已知，CD⊥AB，VN⊥平面ABC，N∈CD，AB平面ABC，∴VN⊥AB.
∴AB⊥平面VNC.
又∵V、M、C、D都在平面VNC内，
∴DM与VN必相交，且AB⊥DM，AB⊥DC.
∴∠MDC为二面角M?AB?C的平面角；
(2)由已知，∠MDC=∠CVN,
在△VNC与△DMC中，∠NCV=∠MCD.
又∠VNC=90°,∴∠DMC=∠VNC=90°,
∴DM⊥VC,又VC⊥AB，∴VC⊥平面AMB.
练习册系列答案
相关题目
（2013•松江区二模）如图，已知ABC-A1B1C1是正三棱柱，它的底面边长和侧棱长都是2．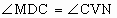
．
．
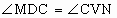