在Rt△SAC中AC=5.SC=10.cosSCA=∴∠SCA=60°.即侧面SBC与底面ABC所成的二面角的大小为60°.(Ⅲ)解:在Rt△SAC中.——青夏教育精英家教网——

摘要：在Rt△SAC中AC=5.SC=10.cosSCA=∴∠SCA=60°.即侧面SBC与底面ABC所成的二面角的大小为60°.(Ⅲ)解:在Rt△SAC中.

网址：http://m.1010jiajiao.com/timu_id_425118[举报]

在Rt△ABC中,AC=BC=1,∠BCA=90°.现将△ABC沿着平面ABC的法向量平移到△A₁B₁C₁位置,已知AA₁=2,分别取A₁B₁、A₁A的中点P、Q.

(1)求的长;

(2)求cos〈〉,cos〈〉,并比较〈〉与〈〉的大小;

(3)求证:AB₁⊥C₁P.

查看习题详情和答案>>

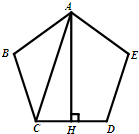如图，正五边形ABCDE的边长为2，甲同学在△ABC中用余弦定理解得AC=

，乙同学在Rt△ACH中解得AC=

，据此可得cos72°的值所在区间为（　　）

A．（0.1，0.2）

B．（0.2，0.3）

C．（0.3，0.4）

D．（0.4，0.5）

查看习题详情和答案>>

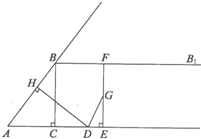如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB_l∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB₁于F，G是EF中点，连接DG．设点D运动的时间为t秒．
（1）当t为何值时，AD=AB，并求出此时DE的长度；
（2）当△DEG与△ACB相似时，求t的值；
（3）以DH所在直线为对称轴，线段AC经轴对称变换后的图形为A′C′．
①当t＞

时，连接C′C，设四边形ACC′A′的面积为S，求S关于t的函数关系式；
②当线段A′C′与射线BB，有公共点时，求t的取值范围（写出答案即可）．

查看习题详情和答案>>

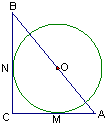（2009•越秀区模拟）（《几何证明选讲》选做题）如图，在Rt△ABC中，∠C=90°，⊙O分别切AC、BC于M、N，圆心O在AB上，⊙O的半径为4，OA=5，则OB的长为

查看习题详情和答案>>

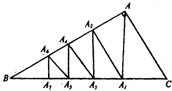如图，在Rt△ABC中，∠BAC=90°，作AA₁⊥BC，A₁A₂⊥AB，A₂A₃⊥BC，A₃A₄⊥AB，A₄A₅⊥BC，A₅A₆⊥AB，A₆A₇⊥BC，A₁，A₂，A₃，A₄，A₅，A₆，A₇分别为垂足：
（1）△CAA₁，△A₁A₂A₃，△A₃A₄A₅，△A₅A₆A₇的周长和面积是否分别成等比数列？试给出证明．
（2）若AB=4，BC=5，分别求出（1）题中4个三角形的周长和△A₁A₂A₃的面积．
（3）如果把题设中的作法一直进行下去，并把所得类同于（1）题中的4个三角形的所有三角形的面积从大到小排成一个数列{S_n}，设AB=c，AC=b，求{S_n}的通项公式和△A₁₁A₁₂A₁₃的面积．查看习题详情和答案>>