题目内容
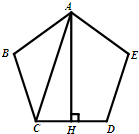 如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得AC=
如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得AC=| 8-8cos108° |
| 1 |
| cos72° |
分析:根据题意,建立方程,再构造函数.利用零点存在定理,确定零点所在区间.
解答:解:根据题意可得
=
∴cos72°×
-1=0
构造函数f(x)=x
-1
∵f(0.3)=0.3×
-1<0,f(0.4)=0.4×
-1>0
∴x所在区间为(0.3,0.4)
即cos72°的值所在区间为(0.3,0.4)
故选C.
| 8-8cos108° |
| 1 |
| cos72° |
∴cos72°×
| 8+8cos72° |
构造函数f(x)=x
| 8+8x |
∵f(0.3)=0.3×
| 10.4 |
| 11.2 |
∴x所在区间为(0.3,0.4)
即cos72°的值所在区间为(0.3,0.4)
故选C.
点评:本题考查解三角形,考查函数思想,考查函数零点的判断,属于中档题.

练习册系列答案
相关题目
 如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得
如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得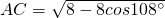 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得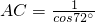 ,据此可得cos72°的值所在区间为
,据此可得cos72°的值所在区间为 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得 ,据此可得cos72°的值所在区间为( )
,据此可得cos72°的值所在区间为( )
 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得 ,据此可得cos72°的值所在区间为( )
,据此可得cos72°的值所在区间为( )