题目内容
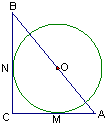（2009•越秀区模拟）（《几何证明选讲》选做题）如图，在Rt△ABC中，∠C=90°，⊙O分别切AC、BC于M、N，圆心O在AB上，⊙O的半径为4，OA=5，则OB的长为| 20 |
| 3 |
| 20 |
| 3 |
分析：先利用圆的切线的性质，可知OMCN为正方形，再利用平行线，可得比例式，从而可得结论．
解答：解：连接OM，ON，则
∵⊙O分别切AC、BC于M、N
∴OM⊥AC，ON⊥BC
∵∠C=90°，
∴OMCN为正方形
∵⊙O的半径为4，OA=5
∴AM=3
∴CA=7
∵ON∥AC
∴
=
∴
=
∴OB=
故答案为：
∵⊙O分别切AC、BC于M、N
∴OM⊥AC，ON⊥BC
∵∠C=90°，
∴OMCN为正方形
∵⊙O的半径为4，OA=5
∴AM=3
∴CA=7
∵ON∥AC
∴
| ON |
| AC |
| OB |
| BA |
∴
| 4 |
| 7 |
| OB |
| OB+5 |
∴OB=
| 20 |
| 3 |
故答案为：
| 20 |
| 3 |
点评：本题以圆为载体，考查圆的切线的性质，解题的关键是利用圆的切线垂直于经过切点的半径．
练习册系列答案
相关题目
（2009•越秀区模拟）如图是一个几何体的三视图．若该几何体的侧面积为8π，则正（主）视图中a=（ ）