题目内容
在Rt△ABC中,AC=BC=1,∠BCA=90°.现将△ABC沿着平面ABC的法向量平移到△A1B1C1位置,已知AA1=2,分别取A1B1、A1A的中点P、Q.(1)求![]() 的长;
的长;
(2)求cos〈![]() 〉,cos〈
〉,cos〈![]() 〉,并比较〈
〉,并比较〈![]() 〉与〈
〉与〈![]() 〉的大小;
〉的大小;
(3)求证:AB1⊥C1P.

解:(1)以C为原点O,建立如图所示的空间直角坐标系O—xyz,则由已知,得
C(0,0,0),A(1,0,0),B(0,1,0),C1(0,0,2),P(![]() ,
,![]() ,2),Q(1,0,1),
,2),Q(1,0,1),
B1(0,1,2),A1(1,0,2).
∴![]() =(1,-1,1),
=(1,-1,1),![]() =(0,1,2),
=(0,1,2),
![]() =(1,-1,2),
=(1,-1,2),![]() =(-1,1,2),
=(-1,1,2),
![]() =(
=(![]() ,
,![]() ,0).
,0).
![]()
(2)![]()
![]()
∴cos〈![]() 〉
〉![]()
又![]() =0-1+4=3,
=0-1+4=3,
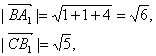
∴cos〈![]() 〉
〉![]()
又![]()
∴〈![]() 〉,〈
〉,〈![]() 〉∈(0,
〉∈(0,![]() ).
).
又y=cosx在(0,![]() )内单调递减,?
)内单调递减,?
∴〈![]() 〉>〈
〉>〈![]() 〉.
〉.
(3)证明:又![]() =(-1,1,2)·(
=(-1,1,2)·(![]() ,
,![]() ,0)=0,
,0)=0,
∴![]() ⊥
⊥![]() ,即AB1⊥C1P.
,即AB1⊥C1P.
绿色通道:
两向量所成的角θ∈[0,π],第(3)问中,将欲证的![]() ⊥
⊥![]() 转化为
转化为![]() ⊥
⊥![]() ,再利用向量垂直的坐标运算就轻易解决了.这种转化思想是数学的重要思想.
,再利用向量垂直的坐标运算就轻易解决了.这种转化思想是数学的重要思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在Rt△ABC中,∠A=90°,∠B=60°,AB=1,若圆O的圆心在直角边AC上,且与AB和BC所在的直线都相切,则圆O的半径是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|


 , ∠B=
, ∠B=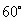 ,
AB=1. 若圆O的圆心在直角边AC上, 且与AB
,
AB=1. 若圆O的圆心在直角边AC上, 且与AB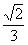 (B)
(B)
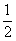
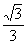 (D)
(D)