摘要：(Ⅰ)证法一:连接AC.∵正四棱柱ABCD―A1B1C1D1的底面是正方形.∴AC⊥BD.又AC⊥D1D.故AC⊥平面BDD1B1∵E.F分别为AB.BC的中点.故EF∥AC.∴EF⊥平面BDD1B1∴平面B1EF⊥平面BDD1B1.证法二:∵BE=BF.∠EBD=∠FBD=45°.∴EF⊥BD.∴平面B1EF⊥平面BDD1B1.(Ⅱ)解:在对角面BDD1B1中.作D1H⊥B1G.垂足为H∵平面B1EF⊥平面BDD1B1.且平面B1EF∩平面BDD1B1=B1G.∴D1H⊥平面B1EF.且垂足为H.∴点D1到平面B1EF的距离d=D1H.解法一:在Rt△D1HB1中.D1H=D1B1?sinD1B1H.
网址：http://m.1010jiajiao.com/timu_id_425106[举报]
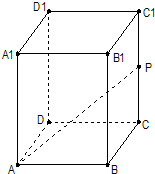（2012•长宁区一模）在正四棱柱ABCD-A1B1C1D1中，已知底面ABCD的边长为2，点P是CC1的中点，直线AP与平面BCC1B1成30°角，求异面直线BC1和AP所成角的大小．（结果用反三角函数值表示）
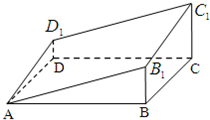（2012•北海一模）过正四棱柱的底面ABCD中顶点A，作与底面成30°角的截面AB1C1D1，截得的多面体如图，已知AB=1，B1B=D1D，则这个多面体的体积为（ ）
和2，它的顶点都在同一个球面上，则该球的表面积为
B. 
C. 
D.
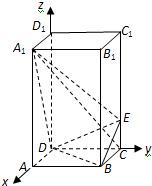如图，在正四棱柱ABC-A1B1C1D1中，DC=DA=2，DD1=4，点E在C1C上，且CE=1．
AB，点E，M分别为A1B，C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N.