Question

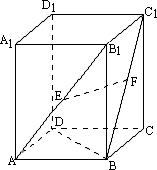
如下图，在正四棱柱ABC-A₁B₁C₁D₁中，AA₁=AB，点E，M分别为A₁B，C₁C的中点，过点A₁，B，M三点的平面A₁BMN交C₁D₁于点N.

（1）求证：EM∥平面A₁B₁C₁D₁；

（2）求二面角B-A₁N-B₁的正切值.

Answer 1

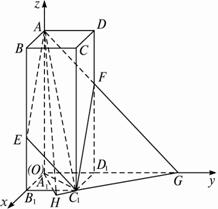
（1）证明：如下图建立空间直角坐标系O-xyz,

设AB=2a，

A₁A=a(a＞0)，则

A₁(2a,0,a),B(2a,2a,0),

C(0,2a,0),C₁(0,2a,a).

∵E为A₁B的中点，M为CC₁的中点，

∴E（2a,a,）,M(0,2a,).

∴=(-2a,a,0).

取平面A₁B₁C₁D₁的法向量，则

=（0,0,a）.

∵·=0，

即与平面A₁B₁C₁D₁的法向量垂直.

∴EM∥平面A₁B₁C₁D₁；

（2）解析：设平面A₁BM的法向量为n₁=(x,y,z)，

又=(0,2a,-a)，=(-2a,0,)，

则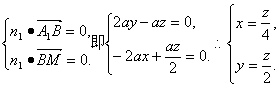

令z=1，则n₁=(,,1)，

而平面A₁B₁C₁D₁的法向量为n₂=(0,0,1)，

设二面角为θ，则|cosθ|=，

又二面角为锐二面角，

∴cosθ=.

∴tanθ=.