摘要:如图9―41.已知A1B1C1―ABC是正三棱柱.D是AC中点.(Ⅰ)证明:AB1∥平面DBC1,假设AB1⊥BC1.求以BC1为棱的DBC1与CBC1为面的二面角α的度数.(文)假设AB1⊥BC1.BC=2.求线段AB1在侧面B1BCC1上的射影长.
网址:http://m.1010jiajiao.com/timu_id_424903[举报]
(本小题满分14分)如图9-3,已知:射线OA为y=kx(k>0,x>0),射线OB为y= -kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
(1)当k为定值时,动点P的纵坐标y是横坐标x的函数,求这个函数y=f(x)的解析式;
 (2)根据k的取值范围,确定y=f(x)的定义域.
(2)根据k的取值范围,确定y=f(x)的定义域.
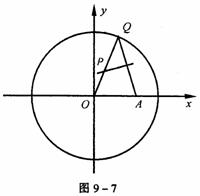
如图9-7,已知圆C:x2+y2=4,A(![]() ,0)是圆内一点。Q是圆上一动点,AQ的垂直平分线交OQ于P,当点Q在圆C上运动一周时,点P的轨迹为曲线E。
,0)是圆内一点。Q是圆上一动点,AQ的垂直平分线交OQ于P,当点Q在圆C上运动一周时,点P的轨迹为曲线E。
(1)求曲线E的方程;
(2)过点O作倾斜角为θ的直线与曲线E交于B1、B2两点,当θ在范围(0,![]() )内变化时,求△AB1B2的面积S(θ)的最大值。
)内变化时,求△AB1B2的面积S(θ)的最大值。
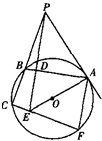 如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF. 如图所示,已知椭圆C的离心率为
如图所示,已知椭圆C的离心率为