题目内容
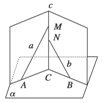
如图9-38,已知平面a ∥平面b ,A、C∈a ,B、D∈b ,E、F分别为AB、CD的中点.求证:EF∥a ,EF∥b .
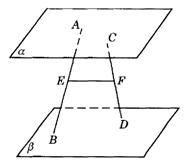
解析:
当AB、CD共面时,平面ABCD∩a =AC,平面ABCD∩b =BD.∵ a ∥b ,∴ AC∥BD.∵ E、F分别为AB、CD的中点,∴ EF∥AC.∵ AC ![]() a ,EF
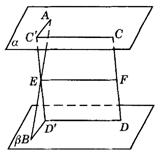
a ,EF ![]() a ,∴ EF∥a ,同理EF∥b .当AB、CD异面时,∵
a ,∴ EF∥a ,同理EF∥b .当AB、CD异面时,∵ ![]() ,∴ 可在平面ECD内过点E作
,∴ 可在平面ECD内过点E作![]() ,与a ,b 分别交于
,与a ,b 分别交于![]() ,
,![]() .平面
.平面![]() ,平面
,平面![]() ,∵ a ∥b ,∴
,∵ a ∥b ,∴ ![]() .∵ E是AB中点,∴ E也是
.∵ E是AB中点,∴ E也是![]() 的中点.平面
的中点.平面![]() ,平面
,平面![]() ,∵ a ∥b ,∴
,∵ a ∥b ,∴ ![]() ,∵ E、F分别为
,∵ E、F分别为![]() 、CD中点,∴
、CD中点,∴ ![]() ,
,![]() .∵
.∵ ![]()
![]() a ,EF
a ,EF ![]() a ,∴ EF∥a ,同理EF∥b .
a ,∴ EF∥a ,同理EF∥b .

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
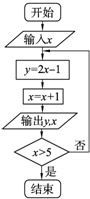 6、如图所示,已知集合A={x|框图中输出的x值},集合B={y|框图中输出的y值},全集U=Z,Z为整数集.当x=-1时(CUA)∩B=( )
6、如图所示,已知集合A={x|框图中输出的x值},集合B={y|框图中输出的y值},全集U=Z,Z为整数集.当x=-1时(CUA)∩B=( ) (2012•大丰市一模)如图所示,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3).
(2012•大丰市一模)如图所示,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3). (2)根据k的取值范围,确定y=f(x)的定义域.
(2)根据k的取值范围,确定y=f(x)的定义域.