Question

如图9-7，已知圆C：x²+y²=4,A(,0)是圆内一点。Q是圆上一动点，AQ的垂直平分线交OQ于P，当点Q在圆C上运动一周时，点P的轨迹为曲线E。

（1）求曲线E的方程；

（2）过点O作倾斜角为θ的直线与曲线E交于B₁、B₂两点，当θ在范围（0，）内变化时，求△AB₁B₂的面积S(θ)的最大值。

Answer 1

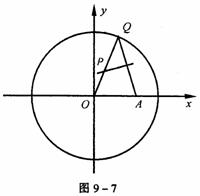
解  （1）∵P在AQ的垂直平分线上，又在半径OQ上，∴|PQ|=|PA|，且|OP|+|PA|=|OQ|=2，

故P点的轨迹是以O、A为焦点，长轴长为2，中心在（，0）的椭圆：

(x-)²+=1

（2）设OB₁=x，则AB₁=2-x，在△OAB₁中，由余弦定理得|AB₁|²=|OB₁|²+|OA|²-2|OB₁|·|OA|

cosθ，

即(2-x)²=x²+3-2x·cosθ，解得x=,

同理可得,

S(θ)=S=S+S

=|OA|·|OB₁|sinθ+|OA|·|OB₂|sin(π-θ)

=|OA|(+)

==≤

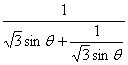当且仅当sinθ=，即θ=arcsin时取等号，

∴当θ=arcsin时，S_max(θ)=。