题目内容
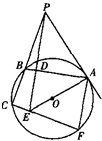 如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.(1)求证:B,C,E,D四点共圆;
(2)当AB=12,tan∠EAF=
| 2 | 3 |
分析:(1)由切割线定理PA2=PB•PC,由已知易得Rt△PAD∽Rt△PEA,可得PA2=PD•PE,于是PB•PC=PD•PE,可得△PBD∽△PEC,因此∠BDP=∠C
即可得出B,C,E,D四点共圆
(2)作OG⊥AB于G,由(1)知∠PBD=∠PEC,利用四点共圆的性质可得∠PBD=∠F,因此∠F=∠PEC,可得PE∥AF.进而得到PE∥OG∥AF,
于是∠AOG=∠EAF.在Rt△AOG中,tan∠AOG=tan∠EAF=
=
,可得OG,再利用勾股定理可得OA=
.
即可得出B,C,E,D四点共圆
(2)作OG⊥AB于G,由(1)知∠PBD=∠PEC,利用四点共圆的性质可得∠PBD=∠F,因此∠F=∠PEC,可得PE∥AF.进而得到PE∥OG∥AF,
于是∠AOG=∠EAF.在Rt△AOG中,tan∠AOG=tan∠EAF=
| 2 |
| 3 |
| 6 |
| OG |
| OG2+AG2 |
解答: 解:(1)由切割线定理PA2=PB•PC
解:(1)由切割线定理PA2=PB•PC
由已知易得Rt△PAD∽Rt△PEA,∴PA2=PD•PE,
∴PA2=PB•PC=PA2=PD•PE,
又∠BPD为公共角,∴△PBD∽△PEC,
∴∠BDP=∠C
∴B,C,E,D四点共圆
(2)作OG⊥AB于G,由(1)知∠PBD=∠PEC,
∵∠PBD=∠F,∴∠F=∠PEC,
∴PE∥AF.
∵AB=12,∴AG=6.
∵PD⊥AB,∴PD∥OG.
∴PE∥OG∥AF,
∴∠AOG=∠EAF.
在Rt△AOG中,tan∠AOG=tan∠EAF=
=
,
∴OG=9∴R=AO=
=3
∴圆O的半径3
.
 解:(1)由切割线定理PA2=PB•PC
解:(1)由切割线定理PA2=PB•PC由已知易得Rt△PAD∽Rt△PEA,∴PA2=PD•PE,
∴PA2=PB•PC=PA2=PD•PE,
又∠BPD为公共角,∴△PBD∽△PEC,
∴∠BDP=∠C
∴B,C,E,D四点共圆
(2)作OG⊥AB于G,由(1)知∠PBD=∠PEC,
∵∠PBD=∠F,∴∠F=∠PEC,
∴PE∥AF.
∵AB=12,∴AG=6.
∵PD⊥AB,∴PD∥OG.
∴PE∥OG∥AF,
∴∠AOG=∠EAF.
在Rt△AOG中,tan∠AOG=tan∠EAF=
| 2 |
| 3 |
| 6 |
| OG |
∴OG=9∴R=AO=
| AG2+OG2 |
| 13 |
∴圆O的半径3
| 13 |
点评:熟练掌握四点共圆的判定与性质、切线的性质、切割线定理、相似三角形的判定与性质、垂径定理等是解题的关键.

练习册系列答案
相关题目

 于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
 时,求圆O的半径.
时,求圆O的半径.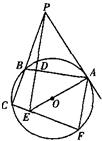
 时,求圆O的半径.
时,求圆O的半径.