如图9―38.在二面角α―l―β中.A.B∈α.C.D∈l.ABCD为矩形.P∈β.PA⊥α.且PA＝AD.M.N依次是AB.PC的中点.(1)求二面角α―l―β的大小,(2)求证:MN⊥AB,(3)——青夏教育精英家教网——

摘要：如图9―38.在二面角α―l―β中.A.B∈α.C.D∈l.ABCD为矩形.P∈β.PA⊥α.且PA＝AD.M.N依次是AB.PC的中点.(1)求二面角α―l―β的大小,(2)求证:MN⊥AB,(3)求异面直线PA与MN所成角的大小.

网址：http://m.1010jiajiao.com/timu_id_424898[举报]

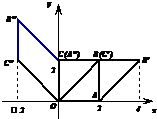（Ⅰ）如图，正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′，平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C''，求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵．
（Ⅱ）在直角坐标系xOy中，圆O的参数方程为

（θ为参数，r＞0）．以O为极点，x轴正半轴为极轴，并取相同的单位长度建立极坐标系，直线l的极坐标方程为ρsin(θ+

．写出圆心的极标，并求当r为何值时，圆O上的点到直线l的最大距离为3．
（Ⅲ）已知a²+2b²+3c²=6，若存在实数a，b，c，使得不等式a+2b+3c＞|x+1|成立，求实数x的取值范围．查看习题详情和答案>>

如图9-38，已知平面a ∥平面b ，A、C∈a ，B、D∈b ，E、F分别为AB、CD的中点．求证：EF∥a ，EF∥b ．

查看习题详情和答案>>

如图9-4，在直四棱柱A₁B₁C₁D₁-ABCD中，当底面四边形ABCD满足条件时，有A₁C⊥B₁D₁(注：填上你认为正确的一种条件即可，不必考虑所有可能的情形).

查看习题详情和答案>>

如图9-4，在直四棱柱A₁B₁C₁D₁-ABCD中，当底面四边形ABCD满足条件时，有A₁C⊥B₁D₁(注：填上你认为正确的一种条件即可，不必考虑所有可能的情形).

查看习题详情和答案>>

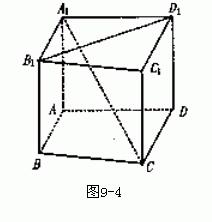
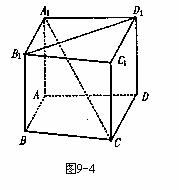
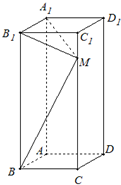（2012•上海模拟）如图所示，在长方体ABCD-A₁B₁C₁D₁中，AB=1，BC=2，CC₁=5，M为棱CC₁上一点．
（1）若C1M=

，求异面直线A₁M和C₁D₁所成角的正切值；
（2）若C₁M=1，试证明：BM⊥平面A₁B₁M．

查看习题详情和答案>>