题目内容
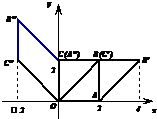 (Ⅰ)如图,正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′,平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C'',求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵.
(Ⅰ)如图,正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′,平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C'',求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵.(Ⅱ)在直角坐标系xOy中,圆O的参数方程为
|
| π |
| 4 |
| ||
| 2 |
(Ⅲ)已知a2+2b2+3c2=6,若存在实数a,b,c,使得不等式a+2b+3c>|x+1|成立,求实数x的取值范围.
分析:(Ⅰ)先设正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵M=
,由于点A(2,0)经矩阵M变换为A''(0,2),C(0,2)经矩阵M变换为C''(-2,2),列出 关于a,b,c,d 的方程式即可解得a,bc,d.从而写出变换对应的矩阵;
(Ⅱ)先写出圆心的极坐标(1,
)和直线的方程,再利用直线与圆的位置关系即可求得圆O上的点到直线的最大距离;
(Ⅲ)先根据由柯西不等式得(a+2b+3c)2≤(a2+2b2+3c2)(1+2+3),得到不等关系|x+1|<6最后解此绝对值不等式即得.
|
(Ⅱ)先写出圆心的极坐标(1,
| 5π |
| 4 |
(Ⅲ)先根据由柯西不等式得(a+2b+3c)2≤(a2+2b2+3c2)(1+2+3),得到不等关系|x+1|<6最后解此绝对值不等式即得.
解答:(Ⅰ)解:设正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵M=
,
如图点A(2,0)经矩阵M变换为A''(0,2),C(0,2)经矩阵M变换为C''(-2,2),
所以
=
,即
(3分)
=
,即
(5分)
解得a=0,c=1,b=-1,d=1,
所以M=
.(7分)
(Ⅱ)解:圆心的极坐标(1,
).(3分)
直线为x+y-1=0,
圆心O(-
,-
)到直线的距离为d=
,(5分)
圆O上的点到直线的最大距离为
+r=3,解得r=2-
.(7分)
(Ⅲ)由柯西不等式得(a+2b+3c)2≤(a2+2b2+3c2)(1+2+3),
当且仅当a=b=c=1时,等号成立.(3分)
故a+2b+3c的最大值为6,故|x+1|<6,(5分)
解得{x|-7<x<5}.(7分)
|
如图点A(2,0)经矩阵M变换为A''(0,2),C(0,2)经矩阵M变换为C''(-2,2),
所以
|
|
|
|
|
|
|
|
解得a=0,c=1,b=-1,d=1,
所以M=
|
(Ⅱ)解:圆心的极坐标(1,
| 5π |
| 4 |
直线为x+y-1=0,
圆心O(-
| ||
| 2 |
| ||
| 2 |
|-
| ||
|
圆O上的点到直线的最大距离为
|-
| ||
|
| ||
| 2 |
(Ⅲ)由柯西不等式得(a+2b+3c)2≤(a2+2b2+3c2)(1+2+3),
当且仅当a=b=c=1时,等号成立.(3分)
故a+2b+3c的最大值为6,故|x+1|<6,(5分)
解得{x|-7<x<5}.(7分)
点评:本题主要考查了二阶矩阵,几种特殊的矩阵变换、考查圆的参数方程、参数方程的概念、绝对值不等式的解法等基础知识,不等式的证明问题,其中涉及到柯西不等式的应用问题,有一定的技巧性,需要同学们柯西不等式非常熟练,属于中档题目.

练习册系列答案
相关题目
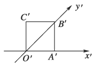
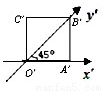
 如图,正方形O'A'B'C'的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积是
如图,正方形O'A'B'C'的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积是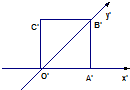 如图,正方形O′A′B′C′的边长为a,它是水平放置的一个平面图形的直观图,则原图形的面积是
如图,正方形O′A′B′C′的边长为a,它是水平放置的一个平面图形的直观图,则原图形的面积是 如图,正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图的周长是( )
如图,正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图的周长是( )