网址:http://m.1010jiajiao.com/timu_id_40753[举报]
一、选择题:本大题共8小题,每小题5分,共40分.
1.C 2.A 3.D 4.B 5.A 6.C 7.D 8.B
二、填空题:本大题共6小题,每小题5分,共30分.
9.0
10..files/image068.gif) 11.24;81
11.24;81
12.(―∞,―1)∪(2,+∞)
13.1;.files/image070.gif) 14.2-|x|
14.2-|x|
注:两空的题目,第一个空2分,第二个空3分.
三、解答题:本大题共6小题,共80分.
15.(本小题满分12分)
(Ⅰ)解:
记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,“该选手通过决赛”为事件C,
则P(A)=.files/image047.gif) ,P(B)=
,P(B)=.files/image073.gif) ,P(C)=
,P(C)=.files/image075.gif) .
.
那么该选手在复赛阶段被淘汰的概率是
P=P(.files/image077.gif) )=P(A)P(
)=P(A)P(.files/image079.gif) )=
)=.files/image047.gif) ×
×.files/image082.gif) .
5分
.
5分
(Ⅱ)解:
ξ可能的取值为1,2,3. 6分
P(ξ-1)=P.files/image084.gif) =1
=1.files/image086.gif)
P(ξ=2)=P(.files/image077.gif) )=P(A)P(
)=P(A)P(.files/image079.gif) )=
)=.files/image088.gif) ,
,
P(ξ=3)=P(AB)=P(A)P(B)=.files/image047.gif) ×
×.files/image090.gif) .
9分
.
9分
ξ的数学期望Eξ=1×.files/image092.gif) 11分
11分
ξ的方差Dξ=.files/image094.gif) 12分
12分
16.(本小题满分12分)
(Ⅰ)解:
∵f.files/image096.gif) =sin2
=sin2.files/image098.gif) (1+sin2
(1+sin2.files/image100.gif) )=
)=.files/image102.gif) 4分
4分
∴sin2.files/image104.gif) .
.
∵.files/image106.gif) ,
,
∴.files/image108.gif)
(Ⅱ)解:
由(Ⅰ)得f(x)=sin2.files/image110.gif) 8分
8分
∵0≤x≤.files/image112.gif) 9分
9分
当2x+.files/image114.gif) =π,即x=
=π,即x=.files/image116.gif) 时,cos
时,cos.files/image118.gif) 取得最小值-1. 11分
取得最小值-1. 11分
∴f(x)在.files/image120.gif) 上的最大值为1,此时x=
上的最大值为1,此时x=.files/image116.gif) 12分
12分
17.(本小题满分14分)
解法一:
(Ⅰ)解:
连结A1D.
.files/image123.gif)
∵ABCD-A1B
∴A1B1⊥平面A1ADD1,
∴A1D是B1D在平A1ADD1上的射影,
∴∠A1DB1是直线B1D和平面A1ADD1所成的角. 2分
在RtΔB.files/image125.gif)
∴∠A1DB1=30°,
即直线B1D和平面A1ADD1,所成角的大小是30° 4分
(Ⅱ)证明:
在Rt△A1AD和Rt△ADE中,
∵.files/image127.gif) ,
,
∴A1AD―△ADE,
∴∠A1DA=∠AED.
∴∠A1DA+∠EAD=∠AED+∠EAD=90°,
∴A1D⊥AE. 7分
由(Ⅰ)知,A1D是B1D在平面A1ADD1上的射影,
根据三垂线定理得,B1D⊥AE. 9分
(Ⅲ)解:
设A1D∩AE=F,连结CF.
∵CD⊥平面A1ADD1,且AE⊥DF,
根据三垂线定理得,AE⊥CF,
∴∠DFC是二面角C-AE-D的平面角. 11分
在Rt△ADE中,由AD?DE=AE?DF.files/image129.gif) .
.
在Rt△FDC中,tan DFC=.files/image131.gif)
∴∠DFC=60°,
即二面角C-AE-D的大小是60° 14分
解法二:
∵ABCD-A1B
∴DA、DC、DD1两两互相垂直.
如图,以D为原点,直线DA,DC,DD1分别为x轴,y轴,z轴,建立空间直角坐标系.
1分
.files/image133.gif)
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),B1(1,1,.files/image021.gif) ).
).
(Ⅰ)解:
连结A1D,∵ABCD-A1B
∴A1B1⊥平面A1ADD1,
∴A1D是B1D在平面A1ADD1上的射影,
∴∠A1DB1是直线B1D和平面A1ADD1所成的角. 4分
∵A1.files/image136.gif) , ∴
, ∴.files/image138.gif)
∴cos.files/image140.gif)
∴∠A1DB1=30°,
即直线B1D和平面A1ADD1所成角的大小是30°, 6分
(Ⅱ)证明:
∵E是DD1的中点 ∴E.files/image142.gif) ,
∴
,
∴.files/image144.gif)
∵.files/image146.gif) =-1+0+1=0,
=-1+0+1=0,
∴B1D⊥AE. 9分
(Ⅲ)解:
设A1D∩AE=F,连结CF.
∵CD⊥平面A1ADD1, 且AE⊥DF;
根据三垂线定理得,AE⊥CF,
∴∠DFC是二面角C-AE-D的平面角. 11分
根据平面几何知识,可求得F.files/image148.gif)
∴.files/image150.gif)
∴cos.files/image152.gif) ,
,
∴二面角C-AE-D的大小是60° 14分
18.(本小题满分14分)
(Ⅰ)解:
∵a1=-3,an=2an-1+2n+3(n≥2,且n∈N*),
∴a2=
a3=
(Ⅱ)证明:
证法一:对于任意n.files/image013.gif) N*,
N*,
∵bn+1-bn=.files/image155.gif) [(an+1-2an)-3]=
[(an+1-2an)-3]=.files/image157.gif) [(2n+1+3)-3]=1,
[(2n+1+3)-3]=1,
∴数列{bn}是首项为.files/image159.gif) =
=.files/image161.gif) =0,公差为1的等差数列.
9分
=0,公差为1的等差数列.
9分
证法二:对于任意n.files/image013.gif) N*,
N*,
∵2bn+1-(bn+bn+2)=2×.files/image163.gif)
.files/image165.gif) =
=.files/image167.gif) (4an+1-4an-an+2-3)
(4an+1-4an-an+2-3)
=.files/image169.gif) [2(an+1-2an)-(an+2-2an+1)-3]=
[2(an+1-2an)-(an+2-2an+1)-3]=.files/image169.gif) [2(2n+1+3)-(2n+2+3)-3]=0,
[2(2n+1+3)-(2n+2+3)-3]=0,
∴2bn+1=bn+bn+2,
∴数例{bn}是首项为.files/image172.gif) =0,公差为b2-b1=1的等差数列.
9分
=0,公差为b2-b1=1的等差数列.
9分
(Ⅲ)解:
由(Ⅱ)得,.files/image062.gif) =0 + (n-1)×1,
=0 + (n-1)×1,
∴an=(n-1)?2n-3(n.files/image013.gif) N*).
10分
N*).
10分
∴Sn=-3+(1×22-3)+(2×23-3)+…+[(n-1)?2n-3],
即Sn=1×22+2×23+3×24+…+(n-1)?2n-3n.
设Tn=1×22+2×23+3×24+…+(n-1)?2n,
则2Tn=1×23+2×24+3×25+…+(n-1)?2n+1,
两式相减得,-Tn=22+23+24+…+2n-(n-1)?2n+1=.files/image175.gif) -(n-1)?2n+1,
-(n-1)?2n+1,
整理得,Tn=4+(n-2)?2n+1,
从而Sn=4+(n-2)?2n+1-3n(n.files/image013.gif) N*).
14分
N*).
14分
19.(本小题满分14分)
(Ⅰ)解:
依题意,直线l的斜率存在,设直线l的方程为y=kx+p,
将其代入x2=2py,消去y整理得x2-2pkx-2p2=0. 2分
设A,B的坐标分别为A(x1,y1),B(x2,y2),则x1x2=-2p2. 3分
将抛物线的方程改写为y=.files/image177.gif) ,求导得y′=
,求导得y′=.files/image179.gif)
所以过点A的切线l1的斜率是k1=.files/image181.gif) ,过点B的切线l2的斜率是k2=
,过点B的切线l2的斜率是k2=.files/image183.gif) ,
,
故k1k2=.files/image185.gif) ,所以直线l1和l2的斜率之积为定值-2. 6分
,所以直线l1和l2的斜率之积为定值-2. 6分
(Ⅱ)解:
设M(x,y).因为直线l1的方程为y-y1=k1(x-x1),即.files/image187.gif) ,
,
同理,直线l2的方程为.files/image189.gif) ,
,
联立这两个方程,消去y得.files/image191.gif) ,
,
整理得(x1-x2).files/image193.gif) =0,注意到x1≠x2,所以x=
=0,注意到x1≠x2,所以x=.files/image195.gif) .
10分
.
10分
此时y=.files/image197.gif) .
12分
.
12分
由(Ⅰ)知,x1+x2=2pk,所以x=.files/image195.gif) =pk
=pk.files/image013.gif) R,
R,
所以点M的轨迹方程是y=-p. 14分
20.(本小题满分14分)
(Ⅰ)解:
f(x)的导数f′(x)=ex-1.
令f′(x)>0,解得x>0;令f′(x)<0,解得x<0.
从而f(x)在(-∞,0)内单调递减,在(0,+∞)内单调递增.
所以,当x=0时,f(x)取得最小值1. 3分
(Ⅱ)解:
因为不等式f(x)>ax的解集为P,且{x|0≤x≤2}.files/image002.gif) P,
P,
所以对于任意x∈[0,2],不等式f(x)>ax恒成立. 4分
由f(x)>ax,得(a+1)x<ex.
当x=0时,上述不等式显然成立,故只需考虑x∈(0,2]的情况. 5分
将(a+1)x<ex变形为a<.files/image201.gif) ,
,
令g(x)=.files/image203.gif) -1,则g(x)的导数g′(x)=
-1,则g(x)的导数g′(x)=.files/image205.gif) ,
,
令g′(x)>0,解得x>1;令g′(x)<0,解得x<1.
从而g(x)在(0,1)内单调递减,在(1,2)内单调递增.
所以,当x=1时,g(x)取得最小值e-1,
从而实数a的取值范围是(-∞,e-1). 8分
(Ⅲ)证明:
由(Ⅰ)得,对于任意x∈R,都有ex-x≥1,即1+x≤ex. 9分
令x=.files/image207.gif) (n∈N*,i=1,2,…,n-1), 则0<1
(n∈N*,i=1,2,…,n-1), 则0<1.files/image207.gif) <
<.files/image210.gif)
∴.files/image212.gif) (i=1,2,…,n-1),
(i=1,2,…,n-1),
即.files/image214.gif) (i=1,2,…,n-1).
(i=1,2,…,n-1).
∴.files/image216.gif)
∵e-(n-1)+e-(n-2)+…+e-1+1=.files/image218.gif) ,
,
∴.files/image220.gif) 14分
14分
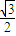 -
- sin2ωx-sinωxcosωx(ω>0),且y=f(x)的图象的一个对称中心到最近的对称轴的距离为
sin2ωx-sinωxcosωx(ω>0),且y=f(x)的图象的一个对称中心到最近的对称轴的距离为 ,
,(Ⅰ)求ω的值
(Ⅱ)求f(x)在区间[
 ]上的最大值和最小值.
]上的最大值和最小值.查看习题详情和答案>>
| 3 |
| 1 |
| 2 |
(1)求函数f(x)的最小值;
(2)设△ABC的内角A、B、C所对边分别为a、b、c,且c=
| 7 |
(3)若
| π |
| 3 |
| π |
| 2 |
| 1 |
| 5 |
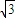 sinxcosx-
sinxcosx- cos2x-1
cos2x-1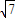 ,f(c)=0,sinB=3sinA,求△ABC的面积;
,f(c)=0,sinB=3sinA,求△ABC的面积;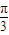 <α<
<α<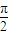 ,f(α)=-
,f(α)=-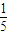 ,求sin2α的值.
,求sin2α的值.