题目内容
已知函数f(x)=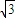 sinxcosx-
sinxcosx- cos2x-1
cos2x-1(1)求函数f(x)的最小值;
(2)设△ABC的内角A、B、C所对边分别为a、b、c,且c=
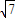 ,f(c)=0,sinB=3sinA,求△ABC的面积;
,f(c)=0,sinB=3sinA,求△ABC的面积;(3)若
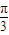 <α<
<α<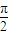 ,f(α)=-
,f(α)=-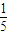 ,求sin2α的值.
,求sin2α的值.
【答案】分析:(1)将f(x)解析式第一项利用二倍角的正弦函数公式化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域即可求出f(x)的最小值;
(2)由C为三角形的内角,求出2C-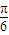 的范围,由f(C)=0,求出sin(2C-
的范围,由f(C)=0,求出sin(2C-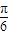 )的值,利用特殊角的三角函数值求出2C-
)的值,利用特殊角的三角函数值求出2C- 的度数,进而确定出C的度数,求出cosC的值,再由c的值,利用余弦定理列出关于a与b的方程,利用正弦定理化简sinB=3sinA,得到a与b的另一个方程,联立两方程求出a与b的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积;
的度数,进而确定出C的度数,求出cosC的值,再由c的值,利用余弦定理列出关于a与b的方程,利用正弦定理化简sinB=3sinA,得到a与b的另一个方程,联立两方程求出a与b的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积;
(3)由第一项确定的解析式及f(α)的值,求出sin(2α- )的值,由α的范围求出2α-
)的值,由α的范围求出2α-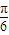 的范围,利用同角三角函数间的基本关系求出cos(2α-
的范围,利用同角三角函数间的基本关系求出cos(2α-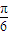 )的值,将所求式子sin2α的角2α变形为(2α-
)的值,将所求式子sin2α的角2α变形为(2α-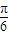 )+
)+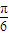 ,利用两角和与差的正弦函数公式及特殊角的三角函数值化简后,将各自的值代入即可求出值.
,利用两角和与差的正弦函数公式及特殊角的三角函数值化简后,将各自的值代入即可求出值.
解答:解:(1)f(x)=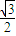 sin2x-
sin2x- cos2x-1=sin(2x-
cos2x-1=sin(2x-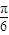 )-1,
)-1,
当2x-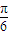 =2kπ-
=2kπ- ,k∈Z,即x=kπ-
,k∈Z,即x=kπ-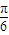 ,k∈Z时,sin(2x-
,k∈Z时,sin(2x-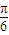 )最小值为-1,
)最小值为-1,
则f(x)取得最小值为-2;
(2)∵C为三角形的内角,∴-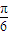 <2C-
<2C-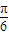 <
<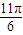 ,
,
又f(C)=sin(2C-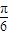 )-1=0,即sin(2C-
)-1=0,即sin(2C-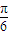 )=1,
)=1,
∴2C-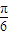 =
=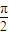 ,即C=
,即C=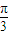 ,又c=
,又c=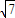 ,
,
∴由余弦定理得:c2=a2+b2-2ab•cosC=a2+b2-ab=(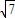 )2=7,
)2=7,
将sinB=3sinA利用正弦定理化简得:b=3a,
解方程组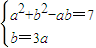 ,得:a=1,b=3,
,得:a=1,b=3,
则S△ABC= absinC=
absinC=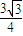 ;
;
(3)f(α)=sin(2α-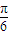 )-1=-
)-1=-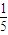 ,即sin(2α-
,即sin(2α-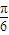 )=
)=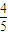 ,
,
∵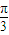 <α<
<α<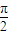 ,∴
,∴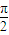 <2α-
<2α-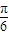 <
<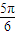 ,
,
∴cos(2α-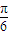 )=
)=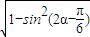 =-
=-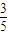 ,
,
则sin2α=sin[(2α- )+
)+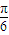 ]=sin(2α-
]=sin(2α-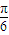 )cos
)cos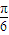 +cos(2α-
+cos(2α- )sin
)sin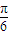 =
=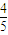 ×
×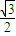 -
-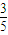 ×
× =
=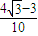 .
.
点评:此题属于解三角形的题型,涉及的知识有:余弦定理,二倍角的正弦函数公式,两角和与差的正弦函数公式,正弦函数的定义域与值域,同角三角函数间的基本关系,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.
(2)由C为三角形的内角,求出2C-
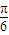 的范围,由f(C)=0,求出sin(2C-
的范围,由f(C)=0,求出sin(2C-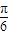 )的值,利用特殊角的三角函数值求出2C-
)的值,利用特殊角的三角函数值求出2C- 的度数,进而确定出C的度数,求出cosC的值,再由c的值,利用余弦定理列出关于a与b的方程,利用正弦定理化简sinB=3sinA,得到a与b的另一个方程,联立两方程求出a与b的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积;
的度数,进而确定出C的度数,求出cosC的值,再由c的值,利用余弦定理列出关于a与b的方程,利用正弦定理化简sinB=3sinA,得到a与b的另一个方程,联立两方程求出a与b的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积;(3)由第一项确定的解析式及f(α)的值,求出sin(2α-
 )的值,由α的范围求出2α-
)的值,由α的范围求出2α-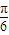 的范围,利用同角三角函数间的基本关系求出cos(2α-
的范围,利用同角三角函数间的基本关系求出cos(2α-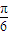 )的值,将所求式子sin2α的角2α变形为(2α-
)的值,将所求式子sin2α的角2α变形为(2α-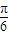 )+
)+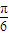 ,利用两角和与差的正弦函数公式及特殊角的三角函数值化简后,将各自的值代入即可求出值.
,利用两角和与差的正弦函数公式及特殊角的三角函数值化简后,将各自的值代入即可求出值.解答:解:(1)f(x)=
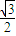 sin2x-
sin2x- cos2x-1=sin(2x-
cos2x-1=sin(2x-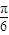 )-1,
)-1,当2x-
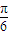 =2kπ-
=2kπ- ,k∈Z,即x=kπ-
,k∈Z,即x=kπ-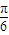 ,k∈Z时,sin(2x-
,k∈Z时,sin(2x-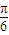 )最小值为-1,
)最小值为-1,则f(x)取得最小值为-2;
(2)∵C为三角形的内角,∴-
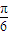 <2C-
<2C-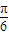 <
<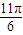 ,
,又f(C)=sin(2C-
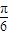 )-1=0,即sin(2C-
)-1=0,即sin(2C-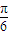 )=1,
)=1,∴2C-
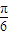 =
=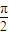 ,即C=
,即C=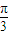 ,又c=
,又c=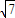 ,
,∴由余弦定理得:c2=a2+b2-2ab•cosC=a2+b2-ab=(
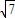 )2=7,
)2=7,将sinB=3sinA利用正弦定理化简得:b=3a,
解方程组
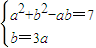 ,得:a=1,b=3,
,得:a=1,b=3,则S△ABC=
 absinC=
absinC=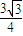 ;
;(3)f(α)=sin(2α-
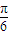 )-1=-
)-1=-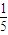 ,即sin(2α-
,即sin(2α-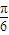 )=
)=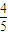 ,
,∵
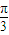 <α<
<α<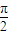 ,∴
,∴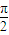 <2α-
<2α-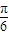 <
<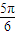 ,
,∴cos(2α-
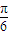 )=
)=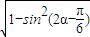 =-
=-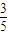 ,
,则sin2α=sin[(2α-
 )+
)+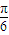 ]=sin(2α-
]=sin(2α-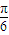 )cos
)cos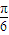 +cos(2α-
+cos(2α- )sin
)sin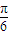 =
=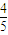 ×
×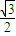 -
-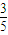 ×
× =
=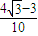 .
.点评:此题属于解三角形的题型,涉及的知识有:余弦定理,二倍角的正弦函数公式,两角和与差的正弦函数公式,正弦函数的定义域与值域,同角三角函数间的基本关系,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
