网址:http://m.1010jiajiao.com/timu_id_40557[举报]
一、选择题:ADBAA BCCDB
二、填空题
11.试卷.files/image216.gif) ; 12.
; 12. 试卷.files/image218.gif) ;
13.
;
13. 试卷.files/image220.gif)
14.(试卷.files/image102.gif) )③⑤ (
)③⑤ (试卷.files/image104.gif) )②⑤
15. (
)②⑤
15. (试卷.files/image102.gif) )
)试卷.files/image222.gif) ; (
; (试卷.files/image104.gif) ) 0
) 0
三、解答题:
16.解:(1)试卷.files/image224.gif)
试卷.files/image226.gif)
试卷.files/image228.gif) …………5分
…………5分
由试卷.files/image128.gif) 成等比数列,知
成等比数列,知试卷.files/image230.gif) 不是最大边
不是最大边
试卷.files/image232.gif) …………6分
…………6分
(2)由余弦定理试卷.files/image234.gif)
试卷.files/image236.gif)
得ac=2 …………11分
试卷.files/image238.gif) =
=试卷.files/image240.gif) …………12分
…………12分
17.解:(Ⅰ)试卷.files/image242.gif) .
.
(Ⅱ)试卷.files/image244.gif) .
.
1当试卷.files/image246.gif) 时,则
时,则试卷.files/image248.gif) .此时轮船
.此时轮船试卷.files/image030.gif) 更安全.
更安全.
2当试卷.files/image251.gif) 时,则
时,则试卷.files/image253.gif) .此时轮船
.此时轮船试卷.files/image030.gif) 和轮船
和轮船试卷.files/image036.gif) 一样安全.
一样安全.
3当试卷.files/image256.gif) 时,则
时,则试卷.files/image258.gif) .此时轮船
.此时轮船试卷.files/image036.gif) 更安全.
更安全.
解:方法一
试卷.files/image261.gif) (Ⅰ)取
(Ⅰ)取试卷.files/image263.gif) 的中点
的中点试卷.files/image265.gif) ,连结
,连结试卷.files/image267.gif) ,由
,由试卷.files/image269.gif) 知
知试卷.files/image271.gif) ,又
,又试卷.files/image273.gif)
试卷.files/image275.gif) ,故
,故试卷.files/image277.gif) ,所以
,所以试卷.files/image279.gif) 即为二面角
即为二面角试卷.files/image167.gif) 的平面角.
的平面角.
在△试卷.files/image282.gif) 中,
中,试卷.files/image284.gif) ,
,试卷.files/image286.gif) ,
,试卷.files/image288.gif) ,
,
由余弦定理有
试卷.files/image290.gif) ,
,
所以二面角试卷.files/image167.gif) 的大小是
的大小是试卷.files/image292.gif) .(6分)
.(6分)
(Ⅱ)由(Ⅰ)知道试卷.files/image294.gif) 平面
平面试卷.files/image282.gif) ,故平面
,故平面试卷.files/image296.gif) 平面
平面试卷.files/image282.gif) ,故
,故试卷.files/image030.gif) 在平面
在平面试卷.files/image299.gif) 上的射影一定在直线
上的射影一定在直线试卷.files/image267.gif) 上,所以点
上,所以点试卷.files/image030.gif) 到平面
到平面试卷.files/image170.gif) 的距离即为△
的距离即为△试卷.files/image282.gif) 的边
的边试卷.files/image267.gif) 上的高.
上的高.
故试卷.files/image301.gif) .
…(12分)
.
…(12分)
19.解: (Ⅰ)∵△ABC的边长为
∵△ADE面积等于△ABC面积的一半,
试卷.files/image172.jpg) ∴
∴试卷.files/image303.gif) x?AEsin60°=
x?AEsin60°=试卷.files/image303.gif) ?
?试卷.files/image305.gif) (
(
解得AE=试卷.files/image307.gif) ,?
,?
在△ADE中,由余弦定理:?
y2=x2+试卷.files/image309.gif) ?
?试卷.files/image307.gif) cos60°,?
cos60°,?
∴y2=x2+试卷.files/image312.gif) -
-
∴y=试卷.files/image314.gif) (a≤x≤
(a≤x≤
(Ⅱ)证明:∵y=试卷.files/image314.gif) (a≤x≤
(a≤x≤
且y=试卷.files/image316.gif) ,设f(t)=t+
,设f(t)=t+试卷.files/image318.gif) (a2≤t≤
(a2≤t≤
当t∈(a2,
f(t1)-f(t2)=(t1+试卷.files/image320.gif) )-(t2+
)-(t2+试卷.files/image322.gif) )
)
=(t1-t2)?试卷.files/image324.gif) ,?
,?
∵a2<t1<t2<
∴t1t2>0,t1-t2>0,t1t2-
∴f(t1)-f(t2)>0,即f(t1)>f(t2)?
∴f(x)在(a2,
同理可得,f(x)在(
又∵f(试卷.files/image326.gif) a时,y有最小值,且ymin=
a时,y有最小值,且ymin=试卷.files/image326.gif) a,此时DE∥BC且AD=
a,此时DE∥BC且AD=试卷.files/image326.gif) a;当t=a2或
a;当t=a2或试卷.files/image328.gif) a,此时DE为AB或AC边上的中线.?
a,此时DE为AB或AC边上的中线.?
试卷.files/image329.gif) 20.解:(Ⅰ)∵
20.解:(Ⅰ)∵试卷.files/image331.gif) ,∴
,∴试卷.files/image333.gif) ,
,
又∵试卷.files/image335.gif) ,∴
,∴试卷.files/image337.gif) ,
,
∴试卷.files/image339.gif) ,
,
∴椭圆的标准方程为试卷.files/image341.gif) .
………(3分)
.
………(3分)
当试卷.files/image343.gif) 的斜率为0时,显然
的斜率为0时,显然试卷.files/image345.gif) =0,满足题意,
=0,满足题意,
当试卷.files/image343.gif) 的斜率不为0时,设
的斜率不为0时,设试卷.files/image343.gif) 方程为
方程为试卷.files/image347.gif) ,
,
代入椭圆方程整理得:试卷.files/image349.gif) .
.
试卷.files/image351.gif) ,
,试卷.files/image353.gif) ,
,试卷.files/image355.gif) .
.
则试卷.files/image357.gif)
试卷.files/image359.gif)
试卷.files/image361.gif) ,
,
而试卷.files/image363.gif)
∴试卷.files/image365.gif) ,从而
,从而试卷.files/image345.gif) .
.
综合可知:对于任意的割线试卷.files/image190.gif) ,恒有
,恒有试卷.files/image345.gif) .
………(8分)
.
………(8分)
(Ⅱ)试卷.files/image370.gif) ,
,
即:试卷.files/image372.gif) ,
,
当且仅当试卷.files/image374.gif) ,即
,即试卷.files/image376.gif) (此时适合于
(此时适合于试卷.files/image378.gif) 的条件)取到等号.
的条件)取到等号.
∴三角形△ABF面积的最大值是试卷.files/image380.gif) . ………………………………(13分)
. ………………………………(13分)
21.解:(Ⅰ)由试卷.files/image382.gif)
试卷.files/image384.gif)
故x>0或x≤-1
f(x)定义域为试卷.files/image386.gif) …………………………(4分)
…………………………(4分)
(Ⅱ)试卷.files/image388.gif)
试卷.files/image390.gif)
下面使用数学归纳法证明:试卷.files/image392.gif)
①在n=1时,a1=1,试卷.files/image303.gif) <a1<2,则n=1时(*)式成立.
<a1<2,则n=1时(*)式成立.
②假设n=k时试卷.files/image395.gif) 成立,
成立,
由试卷.files/image397.gif)
要证明:试卷.files/image399.gif)
只需试卷.files/image401.gif)
只需(2k+1)3≤8k(k+1)2
只需1≤4k2+2k
而4k2+2k≥1在k≥1时恒成立.
试卷.files/image403.gif)
只需证:4k2+11k+8>0,而4k2+11k+8>0在k≥1时恒成立.
于是:试卷.files/image405.gif)
因此试卷.files/image407.gif) 得证.
得证.
综合①②可知(*)式得证.从而原不等式成立. ………………9分
(Ⅲ)要证明:试卷.files/image409.gif)
由(2)可知只需证:
试卷.files/image411.gif) …………(**)
…………(**)
下面用分析法证明:(**)式成立。
要使(**)成立,只需证:试卷.files/image413.gif)
即只需证:(3n-2)3n>(3n-1)3(n-1)
只需证:2n>1
而2n>1在n≥1时显然成立.故(**)式得证:
于是由(**)式可知有:
试卷.files/image415.gif)
因此有:试卷.files/image417.gif)
试卷.files/image419.gif) ……………………………………(13分)
……………………………………(13分)
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求轨迹C的方程;
(Ⅱ)已知点M1为轨迹C上纵坐标为m的点,以M1为圆心满足条件p的圆与x轴相交于点F、A(A在F的右侧),又直线AM1与轨迹C相交于两个不同点M1、M2,当OM1⊥OM2(O为坐标原点)时,求m的值. 查看习题详情和答案>>
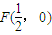 ,且与直线
,且与直线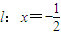 相切;记动圆圆心M的轨迹为C.
相切;记动圆圆心M的轨迹为C.(Ⅰ)求轨迹C的方程;
(Ⅱ)已知点M1为轨迹C上纵坐标为m的点,以M1为圆心满足条件p的圆与x轴相交于点F、A(A在F的右侧),又直线AM1与轨迹C相交于两个不同点M1、M2,当OM1⊥OM2(O为坐标原点)时,求m的值.
查看习题详情和答案>>
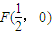 ,且与直线
,且与直线 相切;记动圆圆心M的轨迹为C.
相切;记动圆圆心M的轨迹为C.(Ⅰ)求轨迹C的方程;
(Ⅱ)已知点M1为轨迹C上纵坐标为m的点,以M1为圆心满足条件p的圆与x轴相交于点F、A(A在F的右侧),又直线AM1与轨迹C相交于两个不同点M1、M2,当OM1⊥OM2(O为坐标原点)时,求m的值.
查看习题详情和答案>>
(Ⅰ)判断函数f(x)=
| x |
| 2 |
| sinx |
| 4 |
(Ⅱ)集合M中的元素f(x)具有下面的性质:若f(x)的定义域为D,则对于任意[m,n]⊆D,都存在x0∈[m,n],使得等式f(n)-f(m)=(n-m)f'(x0)成立”,试用这一性质证明:方程f(x)-x=0只有一个实数根;
(Ⅲ)设x1是方程f(x)-x=0的实数根,求证:对于f(x)定义域中任意的x2、x3,当|x2-x1|<1,且|x3-x1|<1时,|f(x3)-f(x2)|<2. 查看习题详情和答案>>