题目内容
设动圆M满足条件p:经过点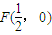 ,且与直线
,且与直线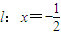 相切;记动圆圆心M的轨迹为C.
相切;记动圆圆心M的轨迹为C.(Ⅰ)求轨迹C的方程;
(Ⅱ)已知点M1为轨迹C上纵坐标为m的点,以M1为圆心满足条件p的圆与x轴相交于点F、A(A在F的右侧),又直线AM1与轨迹C相交于两个不同点M1、M2,当OM1⊥OM2(O为坐标原点)时,求m的值.
【答案】分析:(Ⅰ)可以看出点M的轨迹是以F为焦点,以L为准线的抛物线.,就可求出对应轨迹C的方程;
(Ⅱ)先求出点M1和点点A的坐标以及直线AM1的方程,再把直线方程与抛物线方程联立,求出关于点M1、M2坐标的方程,借助于x1•x2+y1•y2=0即可求出m的值.
解答:解:(Ⅰ)由题得,点M到点F( ,0)的距离与到直线x=-
,0)的距离与到直线x=- 的距离相等.
的距离相等.
所以点M的轨迹是以F为焦点,以L为准线的抛物线.
故所求轨迹C的方程为y2=2x.
(Ⅱ)因为M1在抛物线y2=2x
上,所以M1的坐标为(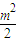 ,m),则点A的坐标为(m2-
,m),则点A的坐标为(m2- ,0),
,0),
又点A在点F右侧,所以必有m2>1,
所以直线AM1的方程为y= (x-m2+
(x-m2+ ).
).
设M1(x1,y1),M2(x2,y2),
由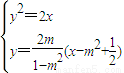 ⇒
⇒ y2-y+
y2-y+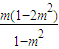 =0,
=0,
显然△>0,所以y1+y2=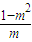 ,y1•y2=1-2m2.x1•x2=
,y1•y2=1-2m2.x1•x2= =
=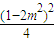 ,
,
当OM1⊥OM2时,有x1•x2+y1•y2=0.
即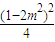 +1-2m2=0.
+1-2m2=0.
又m2>1,∴m2= ⇒m=
⇒m=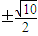 ..
..
点评:本题涉及到求轨迹方程问题.在求轨迹方程时,一般都是利用条件找到一个关于动点的等式,整理即可求出动点的轨迹方程.
(Ⅱ)先求出点M1和点点A的坐标以及直线AM1的方程,再把直线方程与抛物线方程联立,求出关于点M1、M2坐标的方程,借助于x1•x2+y1•y2=0即可求出m的值.
解答:解:(Ⅰ)由题得,点M到点F(
 ,0)的距离与到直线x=-
,0)的距离与到直线x=- 的距离相等.
的距离相等.所以点M的轨迹是以F为焦点,以L为准线的抛物线.
故所求轨迹C的方程为y2=2x.
(Ⅱ)因为M1在抛物线y2=2x
上,所以M1的坐标为(
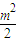 ,m),则点A的坐标为(m2-
,m),则点A的坐标为(m2- ,0),
,0),又点A在点F右侧,所以必有m2>1,
所以直线AM1的方程为y=
 (x-m2+
(x-m2+ ).
).设M1(x1,y1),M2(x2,y2),
由
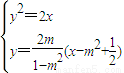 ⇒
⇒ y2-y+
y2-y+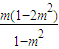 =0,
=0,显然△>0,所以y1+y2=
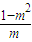 ,y1•y2=1-2m2.x1•x2=
,y1•y2=1-2m2.x1•x2= =
=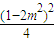 ,
,当OM1⊥OM2时,有x1•x2+y1•y2=0.
即
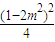 +1-2m2=0.
+1-2m2=0.又m2>1,∴m2=
 ⇒m=
⇒m=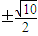 ..
..点评:本题涉及到求轨迹方程问题.在求轨迹方程时,一般都是利用条件找到一个关于动点的等式,整理即可求出动点的轨迹方程.

练习册系列答案
相关题目
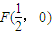 ,且与直线
,且与直线 相切;记动圆圆心M的轨迹为C.
相切;记动圆圆心M的轨迹为C.