网址:http://m.1010jiajiao.com/timu_id_40066[举报]
一.选择题(本大题共12小题,每小题5分,共60分.)
D C B B C D C A C C A B
二.填空题(本大题共4小题,每小题4分,共16分.)
(13) (14)
(14) (15)
(15) (16)―1
(16)―1
三.解答题
(17)(本小题满分12分)
解:(Ⅰ)将一颗骰子先后抛掷2次,此问题中含有36个等可能的基本事件. 2分
记“两数之和为
∴ P(A) .
.
记“两数之和是4的倍数”为事件B,则事件B中含有9个基本事件,
∴ P(B) .
.
∵ 事件A与事件B是互斥事件,∴ 所求概率为  . 8分
. 8分
 (Ⅱ)记“点(x,y)在圆
(Ⅱ)记“点(x,y)在圆  的内部”事件C,则事件C中共含有11个基本事件,∴ P(C)=
的内部”事件C,则事件C中共含有11个基本事件,∴ P(C)= . 12分
. 12分
(18)(本小题满分12分)
解:(Ⅰ)∵ ABC―A1B
∴ BB1⊥AC,BP⊥AC.∴ AC ⊥ 平面PBB1.
又∵M、N分别是AA1、CC1的中点,
∴ MN∥AC.∴ MN ⊥ 平面PBB1 . 4分
(Ⅱ)∵MN∥AC,∴A C ∥ 平面MNQ.
QN是△B1CC1的中位线,∴B
∴平面AB
(Ⅲ)由题意,△MNP的面积 .
.
Q点到平面ACC
∴  .∴三棱锥 Q ― MNP 的体积
.∴三棱锥 Q ― MNP 的体积 . 12分
. 12分
(19)(本小题满分12分)
解:(Ⅰ):

 . 3分
. 3分
依题意, 的周期
的周期 ,且
,且 ,∴
,∴  .∴
.∴ .
.
∴  . 5分
. 5分
∵ 
 [0,
[0, ], ∴
], ∴  ≤
≤ ≤
≤ ,∴
,∴  ≤
≤ ≤1,
≤1,
∴  的最小值为
的最小值为  ,即
,即  ∴
∴
 .
.
∴  . 7分
. 7分
(Ⅱ)∵  =2
=2
 , ∴
, ∴  .
.
又 ∵ ∠ ∈(0,
∈(0, ), ∴ ∠
), ∴ ∠ =
= . 9分
. 9分
在 △ABC中,∵
△ABC中,∵  ,
, ,
,
∴  ,
, .解得
.解得 

 .
.
又 ∵ 0 , ∴
, ∴ 
 . 12分
. 12分
(20)(本小题满分12分)
解:(Ⅰ)对 求导得
求导得  .
.
依题意有  ,且
,且  .∴
.∴  ,且
,且  .
.
解得  . ∴
. ∴  . 6分
. 6分
(Ⅱ)由上问知 ,令
,令 ,得
,得  .
.
显然,当  或
或  时,
时, ;当
;当  时,
时,
 .∴ 函数
.∴ 函数 在
在 和
和 上是单调递增函数,在
上是单调递增函数,在 上是单调递减函数.
上是单调递减函数.
∴ 当
当 时取极大值,极大值是
时取极大值,极大值是 .
.
 当
当 时取极小值,极小值是
时取极小值,极小值是 . 12分
. 12分
 (21)(本小题满分12分)
(21)(本小题满分12分)
解:(Ⅰ)∵  ,
,
∴ .
.
设O关于直线  的
的
对称点为 的横坐标为
的横坐标为  .
.
又易知直线 解得线段
解得线段 的中点坐标
的中点坐标
为(1,-3).∴ .
.
∴ 椭圆方程为  . 5分
. 5分
(Ⅱ)显然直线AN存在斜率,设直线AN的方程为  ,代入
,代入  并整理得:
并整理得: .
.
设点 ,
, ,则
,则 .
.
由韦达定理得  ,
, . 8分
. 8分
∵ 直线ME方程为  ,令
,令 ,得直线ME与x轴的交点
,得直线ME与x轴的交点
的横坐标  .
.
将 ,
, 代入,并整理得
代入,并整理得  . 10分
. 10分
再将韦达定理的结果代入,并整理可得 .
.
∴ 直线ME与 轴相交于定点(
轴相交于定点( ,0). 12分
,0). 12分
(22)(本小题满分14分)
证明:(Ⅰ)∵
 , ∴
, ∴  .
.
显然
 , ∴
, ∴  . 5分
. 5分
∴
 ,
, ,……,
,……, ,
,
将这 个等式相加,得
个等式相加,得  ,∴
,∴  .
7分
.
7分
(Ⅱ)∵
 ,∴
,∴  . 9分
. 9分
∴
 .即
.即  . 11分
. 11分
∴
 ,即
,即
 . 14分
. 14分
直线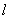 与抛物线
与抛物线 相交于A,B两点,F是抛物线的焦点。
相交于A,B两点,F是抛物线的焦点。
(1)求证:“如果直线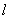 过点T(3,0),那么
过点T(3,0),那么 ”是真命题
”是真命题
(2)设 是抛物线上三点,且
是抛物线上三点,且 成等差数列。当AD的垂直平分线与
成等差数列。当AD的垂直平分线与 轴交于点T(3,0)时,求点B的坐标。
轴交于点T(3,0)时,求点B的坐标。
查看习题详情和答案>>
已知点![]() (0,1),
(0,1),![]() ,直线
,直线![]() 、
、![]() 都是圆
都是圆![]() 的切线(
的切线(![]() 点不在
点不在![]() 轴上). 以原点为顶点,且焦点在
轴上). 以原点为顶点,且焦点在![]() 轴上的抛物线C恰好过点P.
轴上的抛物线C恰好过点P.
(1)求抛物线C的方程;
(2)过点(1,0)作直线![]() 与抛物线C相交于
与抛物线C相交于![]()
![]() 两点,问是否存在定点
两点,问是否存在定点![]() 使
使![]() 为常数?若存在,求出点
为常数?若存在,求出点![]() 的坐标及常数;若不存在,请说明理由.
的坐标及常数;若不存在,请说明理由.
(9分)已知动直线![]() 与抛物线
与抛物线![]() 相交于A点,动点B的坐标是
相交于A点,动点B的坐标是![]()
(Ⅰ)求线段AB的中点M的轨迹![]() 的方程;
的方程;
(Ⅱ)若过点N(1,0)的直线![]() 交轨迹
交轨迹![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 是坐标原点,若
是坐标原点,若![]() 面积为4,求直线
面积为4,求直线![]() 的倾斜角
的倾斜角![]() .
.