题目内容
抛物线y=-
x2与过点M(0,-1)的直线l相交于A、B两点,O为坐标原点,若直线OA和OB的斜率之和为2,求直线l的方程以及线段AB的长.
| 1 | 2 |
分析:设直线l的方程为y=kx-1,交点为A(x1,y1),B(x2,y2),由
,得x2+2kx-2=0,由题意可得kOA+k0B=2,由斜率公式韦达定理可得k的方程,解出k,从而可得直线方程,利用弦长公式可求|AB|.
|
解答:解:由题意,可设直线l的方程为y=kx-1,直线l与双曲线y=-
x2的交点为A(x1,y1),B(x2,y2),
由
,得x2+2kx-2=0,
则
,
∵kOA+k0B=2,
∴
+
=
+
=2,即2k-
=2k-
=k=2,
所以k=2,l的方程为y=2x-1,
|AB|=
•|x1-x2|=
•
=
•
=2
,
所以线段AB的长为2
.
| 1 |
| 2 |
由
|
则
|
∵kOA+k0B=2,
∴
| y1 |
| x1 |
| y2 |
| x2 |
| kx1-1 |
| x1 |
| kx2-1 |
| x2 |
| x1+x2 |
| x1x2 |
| -2k |
| -2 |
所以k=2,l的方程为y=2x-1,
|AB|=
| 1+k2 |
| 1+22 |
| (x1+x2)2-4x1x2 |
=
| 5 |
| (-4)2-4×(-2) |
| 30 |
所以线段AB的长为2
| 30 |
点评:本题考查弦长公式、直线与圆锥曲线的位置关系,考查学生运用知识解决问题的能力.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知P为抛物线y=
x2上的动点,点P在x轴上的射影为M,点A的坐标是(6,
),则|PA|+|PM|的最小值是( )
| 1 |
| 2 |
| 17 |
| 2 |
| A、8 | ||
B、
| ||
| C、10 | ||
D、
|
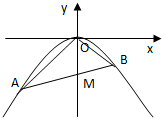 如图,抛物线
如图,抛物线