摘要：∴ 令y=1.可得n1=．-------------7分
网址：http://m.1010jiajiao.com/timu_id_39552[举报]
14、（1+x）n=Cn0+Cn1x+Cn2x2+…+Cnnxn（x∈N*）（1+x）n=C，上式两边对x求导后令x=1，可得结论：Cn1+2Cn2+…+rCnr+nCnn=n•2n-1，利用上述解题思路，可得到许多结论．试问：Cn0+2Cn1+3Cn2+…+（r+1）Cnr+…+（n+1）Cnn=
查看习题详情和答案>>
（n+2）2n-1
．观察下列问题：
已知（1-2x）2013=a0+a1x+a2x2+a3x3+…+a2013x2013，
令x=0，可得a0=1，
令x=1，可得a0+a1+a2+a3+…+a2013=（1-2•1）2013=-1，
令x=-1，可得a0-a1+a2+a3+…-a2013=（1+2•1）2013=32013，
请仿照这种“赋值法”，求出
+
+
+…+
=
查看习题详情和答案>>
已知（1-2x）2013=a0+a1x+a2x2+a3x3+…+a2013x2013，
令x=0，可得a0=1，
令x=1，可得a0+a1+a2+a3+…+a2013=（1-2•1）2013=-1，
令x=-1，可得a0-a1+a2+a3+…-a2013=（1+2•1）2013=32013，
请仿照这种“赋值法”，求出
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2013 |
| 22013 |
-1
-1
．
观察下列问题：
已知（1-2x）2013=a+a1x+a2x2+a3x3+…+a2013x2013，
令x=0，可得a=1，
令x=1，可得a+a1+a2+a3+…+a2013=2013=-1，
令x=-1，可得a-a1+a2+a3+…-a2013=2013=32013，
请仿照这种“赋值法”，求出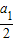
= ．
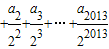查看习题详情和答案>>
已知（1-2x）2013=a+a1x+a2x2+a3x3+…+a2013x2013，
令x=0，可得a=1，
令x=1，可得a+a1+a2+a3+…+a2013=2013=-1，
令x=-1，可得a-a1+a2+a3+…-a2013=2013=32013，
请仿照这种“赋值法”，求出
= ．
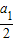
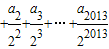查看习题详情和答案>>