题目内容

（1+x）n=Cn+Cn1x+Cn2x2+…+Cnnxn（x∈N*）（1+x）n=C，上式两边对x求导后令x=1，可得结论：Cn1+2Cn2+…+rCnr+nCnn=n•2n-1，利用上述解题思路，可得到许多结论．试问：Cn+2Cn1+3Cn2+…+（r+1）Cnr+…+（n+1）Cnn=    ．
【答案】分析：先设t=Cn+2Cn1+3Cn2+…+（r+1）Cnr+…+（n+1）Cnn再由Cnm=Cnn-m这个性质，将t转化为t=（n+1）Cn+nCn1+（n-1）Cn2+…+（r+1）Cnr+…+Cnn②，两式相加求解．
解答：解：设t=Cn+2Cn1+3Cn2+…+（r+1）Cnr+…+（n+1）Cnn…①
Cnm=Cnn-m
t=（n+1）Cn+nCn1+（n-1）Cn2+…+（r+1）Cnr+…+Cnn…②
由①②相加得：
2t=（n+2）（Cn+Cn1+Cn2+…+Cnr+…+Cnn）=（n+2）2n
∴t=（n+2）2n-1
故答案为：（n+2）2n-1
点评：本题主要考查二项式系数及利用组合数的关系应用倒序相加法求代数式的值．
练习册系列答案
相关题目
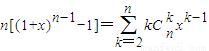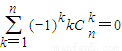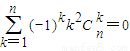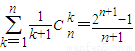若数列{an}的前n项和Sn是（1+x）n二项展开式中各项系数的和（n=1，2，3，…）．
（1）求{an}的通项公式；
（2）若数列{bn}满足b1=-1，bn+1=bn+（2n-1），且cn=
an•bnn
，求数列{cn}的通项及其前n项和Tn．
（3）求证：Tn•Tn+2＜Tn+12．
数列{bn}中，b1=a，b2=a2，其中a＞0，对于函数f(x)=
1
3
(bn+1-bn)x3-(bn-bn-1)x（n≥2）有f′(
1
a
)=0．
（1）求数列{bn}的通项公式；
（2）若
1
2
＜a＜2，cn=
1
2
(bn+
1
bn
)，sn=c1+c2+…+cn，求证：sn＜2n-(
2
2
)n．
请先阅读：
在等式cos2x=2cos2x-1（x∈R）的两边求导，得：（cos2x）′=（2cos2x-1）′，由求导法则，得（-sin2x）•2=4cosx•（-sinx），化简得等式：sin2x=2cosx•sinx．
（1）利用上题的想法（或其他方法），结合等式（1+x）n=Cn+Cn1x+Cn2x2+…+Cnnxn（x∈R，正整数n≥2），证明：．
（2）对于正整数n≥3，求证：
（i）；
（ii）；
（iii）．
请先阅读：
在等式cos2x=2cos2x-1（x∈R）的两边求导，得：（cos2x）′=（2cos2x-1）′，由求导法则，得（-sin2x）•2=4cosx•（-sinx），化简得等式：sin2x=2cosx•sinx．
（1）利用上题的想法（或其他方法），结合等式（1+x）n=Cn+Cn1x+Cn2x2+…+Cnnxn（x∈R，正整数n≥2），证明：．
（2）对于正整数n≥3，求证：
（i）；
（ii）；
（iii）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网