网址:http://m.1010jiajiao.com/timu_id_390924[举报]
已知向量 ,且
,且 ,A为锐角,求:
,A为锐角,求:
(1)角A的大小;
(2)求函数 的单调递增区间和值域.
的单调递增区间和值域.
【解析】第一问中利用 ,解得
,解得 又A为锐角
又A为锐角

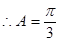
第二问中,
由 解得单调递增区间为
解得单调递增区间为
解:(1) ……………………3分
……………………3分
 又A为锐角
又A为锐角

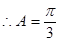 ……………………5分
……………………5分
(2)
……………………8分
由 解得单调递增区间为
解得单调递增区间为
……………………10分

查看习题详情和答案>>
| f(x1)+f(x2) |
| 2 |
(1)判断函数f(x)=x+1,x∈[-1,3]是否为“和谐函数”?答:
(2)请先学习下面的证明方法:
证明:函数g(x)=lgx,x∈[10,100]为“和谐函数”,
| 3 |
| 2 |
证明过程如下:对任意x1∈[10,100],令
| g(x1)+g(x2) |
| 2 |
| 3 |
| 2 |
| lgx1+lgx2 |
| 2 |
| 3 |
| 2 |
得x2=
| 1000 |
| x1 |
| 1000 |
| x1 |
| 1000 |
| x1 |
| g(x)+g(x2) |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
参照上述证明过程证明:函数h(x)=2x,x∈(1,3)为“和谐函数”;
(3)写出一个不是“和谐函数”的函数,并作出证明.
把函数 的图象按向量
的图象按向量 平移得到函数
平移得到函数 的图象.
的图象.
(1)求函数 的解析式; (2)若
的解析式; (2)若 ,证明:
,证明: .
.
【解析】本试题主要考查了函数 平抑变换和运用函数思想证明不等式。第一问中,利用设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 ,便可以得到结论。第二问中,令
,便可以得到结论。第二问中,令 ,然后求导,利用最小值大于零得到。
,然后求导,利用最小值大于零得到。
(1)解:设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 证明:令 ,……6分
,……6分
则 ……8分
……8分
 ,∴
,∴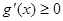 ,∴
,∴ 在
在 上单调递增.……10分
上单调递增.……10分
故 ,即
,即
查看习题详情和答案>>
设函数 .
.
(I)求 的单调区间;
的单调区间;
(II)当0<a<2时,求函数 在区间
在区间 上的最小值.
上的最小值.
【解析】第一问定义域为真数大于零,得到 .
. .
.
令 ,则
,则 ,所以
,所以 或
或 ,得到结论。
,得到结论。
第二问中, (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .
.
对参数讨论的得到最值。
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
(I)定义域为 . ………………………1分
. ………………………1分
 .
.
令 ,则
,则 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因为定义域为 ,所以
,所以 .
.
令 ,则
,则 ,所以
,所以 .
.
因为定义域为 ,所以
,所以 . ………………………5分
. ………………………5分
所以函数的单调递增区间为 ,
,
单调递减区间为 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
①当 ,即
,即 时,
时,
在区间 上,
上, 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
所以 . ………………………10分
. ………………………10分
②当 ,即
,即 时,
时, 在区间
在区间 上为减函数.
上为减函数.
所以 .
.
综上所述,当 时,
时, ;
;
当 时,
时,
查看习题详情和答案>>