摘要：∴对.常数A,B,都有

网址：http://m.1010jiajiao.com/timu_id_390517[举报]

已知常数a、b都是正整数，函数f(x)=

（x＞0），数列{a_n}满足a₁=a，

)（n∈N^*）
（1）求数列{a_n}的通项公式；
（2）若a=8b，且等比数列{b_n}同时满足：①b₁=a₁，b₂=a₅；②数列{b_n}的每一项都是数列{a_n}中的某一项．试判断数列{b_n}是有穷数列或是无穷数列，并简要说明理由；
（3）对问题（2）继续探究，若b₂=a_m（m＞1，m是常数），当m取何正整数时，数列{b_n}是有穷数列；当m取何正整数时，数列{b_n}是无穷数列，并说明理由．

查看习题详情和答案>>

已知常数a、b都是正整数，函数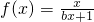 $数学公式$ （x＞0），数列{a_n}满足a₁=a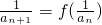， $数学公式$ （n∈N^*）
（1）求数列{a_n}的通项公式；
（2）若a=8b，且等比数列{b_n}同时满足：①b₁=a₁，b₂=a₅；②数列{b_n}的每一项都是数列{a_n}中的某一项．试判断数列{b_n}是有穷数列或是无穷数列，并简要说明理由；
（3）对问题（2）继续探究，若b₂=a_m（m＞1，m是常数），当m取何正整数时，数列{b_n}是有穷数列；当m取何正整数时，数列{b_n}是无穷数列，并说明理由．

查看习题详情和答案>>

已知常数a、b都是正整数，函数f(x)=

（x＞0），数列{a_n}满足a₁=a，

)（n∈N^*）
（1）求数列{a_n}的通项公式；
（2）若a=8b，且等比数列{b_n}同时满足：①b₁=a₁，b₂=a₅；②数列{b_n}的每一项都是数列{a_n}中的某一项．试判断数列{b_n}是有穷数列或是无穷数列，并简要说明理由；
（3）对问题（2）继续探究，若b₂=a_m（m＞1，m是常数），当m取何正整数时，数列{b_n}是有穷数列；当m取何正整数时，数列{b_n}是无穷数列，并说明理由．

查看习题详情和答案>>

对于函数f（x），如果存在函数g（x）=ax+b（a，b为常数），使得对于区间D上的任意实数x都有f（x）≤g（x）成立，则称g（x）为函数f（x）区间D上的一个“覆盖函数”．设f（x）=-2xlnx-x²，g（x）=-ax+3．若g（x）为函数f（x）在区间（0，+∞）上的一个“覆盖函数”，则实数a的取值范围是（　　）

查看习题详情和答案>>

函数y=f（x）与函数y=g（x）有相同的定义域，且都不是常函数，对定义域内的任何x，有f（x）+f（-x）=0，g（x）g（-x）=1，且g（x）≠1，则F（x）=

+f(x)是（　　）

C．既是奇函数又是偶函数

D．既不是奇函数也不是偶函数

查看习题详情和答案>>