题目内容
已知常数a、b都是正整数,函数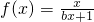 (x>0),数列{an}满足a1=a,
(x>0),数列{an}满足a1=a,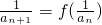 (n∈N*)
(n∈N*)
(1)求数列{an}的通项公式;
(2)若a=8b,且等比数列{bn}同时满足:①b1=a1,b2=a5;②数列{bn}的每一项都是数列{an}中的某一项.试判断数列{bn}是有穷数列或是无穷数列,并简要说明理由;
(3)对问题(2)继续探究,若b2=am(m>1,m是常数),当m取何正整数时,数列{bn}是有穷数列;当m取何正整数时,数列{bn}是无穷数列,并说明理由.
解:(1)∵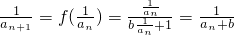
∴an+1=an+b,∴数列{an}是以b为公差的等差数列
∵a1=a,∴an=a+(n-1)b
(2)当a=8b时,an=(n+7)b
∴b1=8b,b2=12b,∴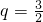 ,∴
,∴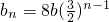
∴b3=18b,b4=27b,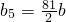
显然, 不是整数,即b5∉{an},∴{bn}是项数最多为4的有穷数列
不是整数,即b5∉{an},∴{bn}是项数最多为4的有穷数列
(3)∵b2=(m+7)b,∴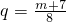 ,此时
,此时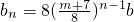
i)当m=8k+1(k∈N)时,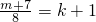 为正整数,
为正整数,
此时{bn}中每一项均为{an}中的项,∴{bn}为无穷数列;
ii)当m=8k+5(k∈N)时,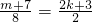
此时当n=1,2,3,4, 为大于8的正整数,
为大于8的正整数,
但n=5时,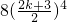 不是正整数,∴此时{bn}是项数最多为4的有穷数列;
不是正整数,∴此时{bn}是项数最多为4的有穷数列;
iii)当m=8k+2,+3,+4,+6,+7,+8(k∈N)时,
此时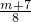 为分母是4或8的最简分数,
为分母是4或8的最简分数,
只有当n=1,2时, 才是大于8的正整数,
才是大于8的正整数,
而当n≥3时, 均为分数,∵{bn}仅有两项,∴此时{bn}不能构成等比数列.
均为分数,∵{bn}仅有两项,∴此时{bn}不能构成等比数列.
分析:(1)由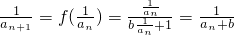 可得an+1=an+b,,从而可证数列{an}是以b为公差的等差数列,进而可求通项
可得an+1=an+b,,从而可证数列{an}是以b为公差的等差数列,进而可求通项
(2)当a=8b时,可得an=(n+7)b,则b1=8b,b2=12b,则有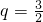 ,可求
,可求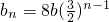 ,由b3=18b,b4=27b,
,由b3=18b,b4=27b,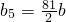 可得b5∉{an
可得b5∉{an
从而可判断
(3)由b2=(m+7)b,可得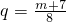 ,此时
,此时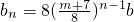
分别就进行讨论(i)当m=8k+1(k∈N)时,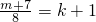 为正整数,(ii)当m=8k+5(k∈N)时,
为正整数,(ii)当m=8k+5(k∈N)时,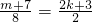 (iii)当m=8k+2,+3,+4,+6,+7,+8(k∈N)
(iii)当m=8k+2,+3,+4,+6,+7,+8(k∈N)
点评:本题主要考查了等差数列的及等比的项公式及数列知识的综合应用,解题的关键是考试具备一定的逻辑推理与计算的能力.
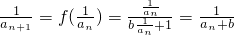
∴an+1=an+b,∴数列{an}是以b为公差的等差数列
∵a1=a,∴an=a+(n-1)b
(2)当a=8b时,an=(n+7)b
∴b1=8b,b2=12b,∴
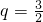 ,∴
,∴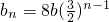
∴b3=18b,b4=27b,
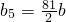
显然,
 不是整数,即b5∉{an},∴{bn}是项数最多为4的有穷数列
不是整数,即b5∉{an},∴{bn}是项数最多为4的有穷数列(3)∵b2=(m+7)b,∴
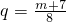 ,此时
,此时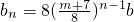
i)当m=8k+1(k∈N)时,
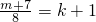 为正整数,
为正整数,此时{bn}中每一项均为{an}中的项,∴{bn}为无穷数列;
ii)当m=8k+5(k∈N)时,
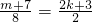
此时当n=1,2,3,4,
 为大于8的正整数,
为大于8的正整数,但n=5时,
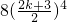 不是正整数,∴此时{bn}是项数最多为4的有穷数列;
不是正整数,∴此时{bn}是项数最多为4的有穷数列;iii)当m=8k+2,+3,+4,+6,+7,+8(k∈N)时,
此时
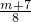 为分母是4或8的最简分数,
为分母是4或8的最简分数,只有当n=1,2时,
 才是大于8的正整数,
才是大于8的正整数,而当n≥3时,
 均为分数,∵{bn}仅有两项,∴此时{bn}不能构成等比数列.
均为分数,∵{bn}仅有两项,∴此时{bn}不能构成等比数列.分析:(1)由
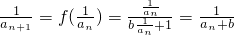 可得an+1=an+b,,从而可证数列{an}是以b为公差的等差数列,进而可求通项
可得an+1=an+b,,从而可证数列{an}是以b为公差的等差数列,进而可求通项(2)当a=8b时,可得an=(n+7)b,则b1=8b,b2=12b,则有
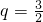 ,可求
,可求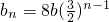 ,由b3=18b,b4=27b,
,由b3=18b,b4=27b,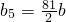 可得b5∉{an
可得b5∉{an从而可判断
(3)由b2=(m+7)b,可得
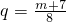 ,此时
,此时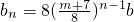
分别就进行讨论(i)当m=8k+1(k∈N)时,
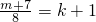 为正整数,(ii)当m=8k+5(k∈N)时,
为正整数,(ii)当m=8k+5(k∈N)时,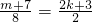 (iii)当m=8k+2,+3,+4,+6,+7,+8(k∈N)
(iii)当m=8k+2,+3,+4,+6,+7,+8(k∈N)点评:本题主要考查了等差数列的及等比的项公式及数列知识的综合应用,解题的关键是考试具备一定的逻辑推理与计算的能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目