摘要:(1)求证:当时.不等式对于恒成立 .
网址:http://m.1010jiajiao.com/timu_id_390303[举报]
(Ⅰ)求证:当a≥1时,不等式ex-x-1≤![]() 对于x∈R恒成立;
对于x∈R恒成立;
(Ⅱ)对于在(0,1)中的任一个常数a,问是否存在x0>0使得ex0-x0-1>![]() 成立?如果存在,求出符合条件的一个x0;否则说明理由.
成立?如果存在,求出符合条件的一个x0;否则说明理由.
(1)求证:当a≥1时,不等式ex-x-1≤
对于n∈R恒成立.
(2)对于在(0,1)中的任一个常数a,问是否存在x0>0使得ex0-x0-1≤
成立?如果存在,求出符合条件的一个x0;否则说明理由.
查看习题详情和答案>>
| ax2e|x| |
| 2 |
(2)对于在(0,1)中的任一个常数a,问是否存在x0>0使得ex0-x0-1≤
| ax02ex0 |
| 2 |
(1)求证:当a≥1时,不等式ex-x-1≤
对于n∈R恒成立.
(2)对于在(0,1)中的任一个常数a,问是否存在x0>0使得ex0-x0-1≤
成立?如果存在,求出符合条件的一个x0;否则说明理由.
查看习题详情和答案>>
| ax2e|x| |
| 2 |
(2)对于在(0,1)中的任一个常数a,问是否存在x0>0使得ex0-x0-1≤
| ax02ex0 |
| 2 |
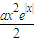 对于n∈R恒成立.
对于n∈R恒成立.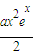 成立?如果存在,求出符合条件的一个x;否则说明理由.
成立?如果存在,求出符合条件的一个x;否则说明理由.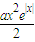 对于n∈R恒成立.
对于n∈R恒成立.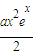 成立?如果存在,求出符合条件的一个x;否则说明理由.
成立?如果存在,求出符合条件的一个x;否则说明理由.