题目内容
(1)求证:当a≥1时,不等式ex-x-1≤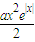 对于n∈R恒成立.
对于n∈R恒成立.(2)对于在(0,1)中的任一个常数a,问是否存在x>0使得ex-x-1≤
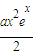 成立?如果存在,求出符合条件的一个x;否则说明理由.
成立?如果存在,求出符合条件的一个x;否则说明理由.
【答案】分析:(1):分x≥0和x<0讨论:(Ⅰ)在x≥0时,要使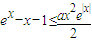 成立;(Ⅱ)在x≤0时,要使
成立;(Ⅱ)在x≤0时,要使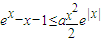 成立.利用导数研究函数的单调性,从而得到,原不等式
成立.利用导数研究函数的单调性,从而得到,原不等式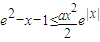 在a≥1时,恒成立;
在a≥1时,恒成立;
(2)先将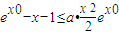 变形为
变形为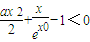 ,要找一个X>0,使此式成立,只需找到函数
,要找一个X>0,使此式成立,只需找到函数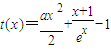 的最小值,满足t(x)min<0即可,对t(x)求导数,研究其单调性和最值,最后得出可找到一个常数x=-lna(0<a<1),使得不等式成立.
的最小值,满足t(x)min<0即可,对t(x)求导数,研究其单调性和最值,最后得出可找到一个常数x=-lna(0<a<1),使得不等式成立.
解答:解:(1)证明:(Ⅰ)在x≥0时,要使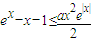 成立.
成立.
只需证: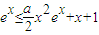 即需证:
即需证: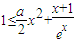 ①
①
令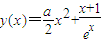 ,求导数
,求导数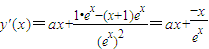
∴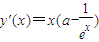 ,又a≥1,求x≥0,故y'(x)≥0
,又a≥1,求x≥0,故y'(x)≥0
∴y(x)为增函数,故y(x)≥y(0)=1,从而①式得证
(Ⅱ)在x≤0时,要使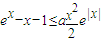 成立.
成立.
只需证: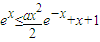 ,即需证:
,即需证: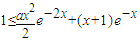 ②
②
令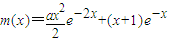 ,求导数得m'(x)=-xe-2x[ex+a(x-1)]
,求导数得m'(x)=-xe-2x[ex+a(x-1)]
而φ(x)=ex+a(x-1)在x≤0时为增函数
故φ(x)≤φ(0)=1-a≤0,从而m(x)≤0
∴m(x)在x≤0时为减函数,则m(x)≥m(0)=1,从而②式得证
由于①②讨论可知,原不等式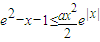 在a≥1时,恒成立…(6分)
在a≥1时,恒成立…(6分)
(2)解:将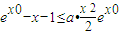 变形为
变形为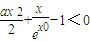 ③
③
要找一个X>0,使③式成立,只需找到函数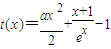 的最小值,
的最小值,
满足t(x)min<0即可,对t(x)求导数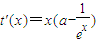
令t'(x)=0得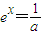 ,则x=-lna,取X=-lna
,则x=-lna,取X=-lna
在0<x<-lna时,t'(x)<0,在x>-lna时,t'(x)>0t(x)在x=-lna时,取得最小值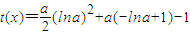
下面只需证明: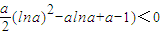 ,在0<a<1时成立即可
,在0<a<1时成立即可
又令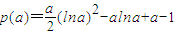 ,对p(a)关于a求导数
,对p(a)关于a求导数
则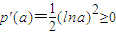 ,从而p(a)为增函数
,从而p(a)为增函数
则p(a)<p(1)=0,从而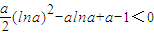 得证
得证
于是t(x)的最小值t(-lna)<0
因此可找到一个常数x=-lna(0<a<1),使得③式成立 …(14分)
点评:利用导数工具讨论函数的单调性,是求函数的值域和最值的常用方法,考查了分类讨论的思想与转化的思想.解决本题同时应注意研究导函数的单调性得出导数的正负,从而得出原函数的单调性的技巧.
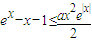 成立;(Ⅱ)在x≤0时,要使
成立;(Ⅱ)在x≤0时,要使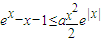 成立.利用导数研究函数的单调性,从而得到,原不等式
成立.利用导数研究函数的单调性,从而得到,原不等式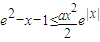 在a≥1时,恒成立;
在a≥1时,恒成立;(2)先将
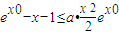 变形为
变形为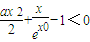 ,要找一个X>0,使此式成立,只需找到函数
,要找一个X>0,使此式成立,只需找到函数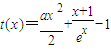 的最小值,满足t(x)min<0即可,对t(x)求导数,研究其单调性和最值,最后得出可找到一个常数x=-lna(0<a<1),使得不等式成立.
的最小值,满足t(x)min<0即可,对t(x)求导数,研究其单调性和最值,最后得出可找到一个常数x=-lna(0<a<1),使得不等式成立.解答:解:(1)证明:(Ⅰ)在x≥0时,要使
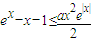 成立.
成立.只需证:
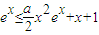 即需证:
即需证: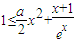 ①
①令
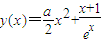 ,求导数
,求导数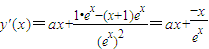
∴
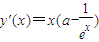 ,又a≥1,求x≥0,故y'(x)≥0
,又a≥1,求x≥0,故y'(x)≥0∴y(x)为增函数,故y(x)≥y(0)=1,从而①式得证
(Ⅱ)在x≤0时,要使
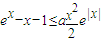 成立.
成立.只需证:
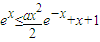 ,即需证:
,即需证: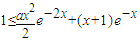 ②
②令
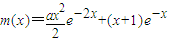 ,求导数得m'(x)=-xe-2x[ex+a(x-1)]
,求导数得m'(x)=-xe-2x[ex+a(x-1)]而φ(x)=ex+a(x-1)在x≤0时为增函数
故φ(x)≤φ(0)=1-a≤0,从而m(x)≤0
∴m(x)在x≤0时为减函数,则m(x)≥m(0)=1,从而②式得证
由于①②讨论可知,原不等式
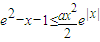 在a≥1时,恒成立…(6分)
在a≥1时,恒成立…(6分)(2)解:将
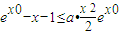 变形为
变形为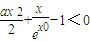 ③
③要找一个X>0,使③式成立,只需找到函数
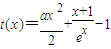 的最小值,
的最小值,满足t(x)min<0即可,对t(x)求导数
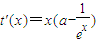
令t'(x)=0得
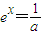 ,则x=-lna,取X=-lna
,则x=-lna,取X=-lna在0<x<-lna时,t'(x)<0,在x>-lna时,t'(x)>0t(x)在x=-lna时,取得最小值
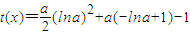
下面只需证明:
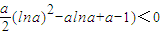 ,在0<a<1时成立即可
,在0<a<1时成立即可又令
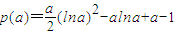 ,对p(a)关于a求导数
,对p(a)关于a求导数则
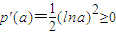 ,从而p(a)为增函数
,从而p(a)为增函数则p(a)<p(1)=0,从而
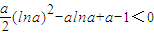 得证
得证于是t(x)的最小值t(-lna)<0
因此可找到一个常数x=-lna(0<a<1),使得③式成立 …(14分)
点评:利用导数工具讨论函数的单调性,是求函数的值域和最值的常用方法,考查了分类讨论的思想与转化的思想.解决本题同时应注意研究导函数的单调性得出导数的正负,从而得出原函数的单调性的技巧.

练习册系列答案
相关题目
 ,则称f(x)是R上凹函数.已知二次函数f(x)=ax2+x(a∈R,且a≠0).
,则称f(x)是R上凹函数.已知二次函数f(x)=ax2+x(a∈R,且a≠0).