摘要：所以k的取值范围为k≤1.--------6分
网址：http://m.1010jiajiao.com/timu_id_390180[举报]
给出下列命题：
①函数
的最小值为5；
②若直线y=kx+1与曲线y=|x|有两个交点，则k的取值范围是-1≤k≤1；
③若直线m被两平行线l1：x-y+1=0与l2：x-y+3=0所截得的线段的长为2
，则m的倾斜角可以是15°或75°
④设Sn是公差为d（d≠0）的无穷等差数列{an}的前n项和，若对任意n∈N*，均有Sn＞0，则数列{Sn}是递增数列
⑤设△ABC的内角A．B．C所对的边分别为a，b，c，若三边的长为连续的三个正整数，且A＞B＞C，3b=20acosA则sinA：sinB：sinC为6：5：4
其中所有正确命题的序号是 ． 查看习题详情和答案>>
①函数
的最小值为5；②若直线y=kx+1与曲线y=|x|有两个交点，则k的取值范围是-1≤k≤1；
③若直线m被两平行线l1：x-y+1=0与l2：x-y+3=0所截得的线段的长为2
，则m的倾斜角可以是15°或75°④设Sn是公差为d（d≠0）的无穷等差数列{an}的前n项和，若对任意n∈N*，均有Sn＞0，则数列{Sn}是递增数列
⑤设△ABC的内角A．B．C所对的边分别为a，b，c，若三边的长为连续的三个正整数，且A＞B＞C，3b=20acosA则sinA：sinB：sinC为6：5：4
其中所有正确命题的序号是 ． 查看习题详情和答案>>
给出下列命题：
①函数y=
+
的最小值为5；
②若直线y=kx+1与曲线y=|x|有两个交点，则k的取值范围是-1≤k≤1；
③若直线m被两平行线l1：x-y+1=0与l2：x-y+3=0所截得的线段的长为2
，则m的倾斜角可以是15°或75°
④设Sn是公差为d（d≠0）的无穷等差数列{an}的前n项和，若对任意n∈N*，均有Sn＞0，则数列{Sn}是递增数列
⑤设△ABC的内角A．B．C所对的边分别为a，b，c，若三边的长为连续的三个正整数，且A＞B＞C，3b=20acosA则sinA：sinB：sinC为6：5：4
其中所有正确命题的序号是
查看习题详情和答案>>
①函数y=
| x2-8x+20 |
| x2+1 |
②若直线y=kx+1与曲线y=|x|有两个交点，则k的取值范围是-1≤k≤1；
③若直线m被两平行线l1：x-y+1=0与l2：x-y+3=0所截得的线段的长为2
| 2 |
④设Sn是公差为d（d≠0）的无穷等差数列{an}的前n项和，若对任意n∈N*，均有Sn＞0，则数列{Sn}是递增数列
⑤设△ABC的内角A．B．C所对的边分别为a，b，c，若三边的长为连续的三个正整数，且A＞B＞C，3b=20acosA则sinA：sinB：sinC为6：5：4
其中所有正确命题的序号是
①③④⑤
①③④⑤
．
如下图,A、B是两个定点,|AB|=4,动点M到A点的距离是6,线段MB的垂直平分线l交MA于点P,直线l′垂直于AB,且B到l′的距离是
.若以AB所在直线为x轴,AB的中垂线为y轴建立直角坐标系.
.若以AB所在直线为x轴,AB的中垂线为y轴建立直角坐标系.
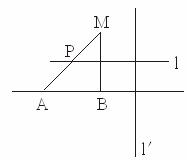
(1)求证:点P到点B的距离与到直线l′的距离之比为定值.
(2)若P点到A、B两点的距离之积为m,当m取最大值时,求P点的坐标.
(3)设直线y=kx+m(k≠0)与点P所在曲线相交于不同两点C、D,定点G(0,－
),则使|GC|=|GD|的正数m是否存在?若存在,则求出其取值范围;若不存在,请说明理由.
某学校高三年级有学生1000名，经调查研究，其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼（称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学．
（Ⅰ）求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
（Ⅱ）测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如右图：
（ⅰ）统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170）的中点值为165）作为代表．据此，计算这100名学生身高数据的期望μ及标准差φ（精确到0.1）；
（ⅱ）若总体服从正态分布，以样本估计总体，据此，估计该年级身高在（158.6，181.4）范围中的学生的人数．
（Ⅲ）如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
体育锻炼与身高达标2×2列联表
（ⅰ）完成上表；
（ⅱ）请问有多大的把握认为体育锻炼与身高达标有关系？
参考公式：K2=
，参考数据：
查看习题详情和答案>>
（Ⅰ）求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
（Ⅱ）测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如右图：
（ⅰ）统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170）的中点值为165）作为代表．据此，计算这100名学生身高数据的期望μ及标准差φ（精确到0.1）；
（ⅱ）若总体服从正态分布，以样本估计总体，据此，估计该年级身高在（158.6，181.4）范围中的学生的人数．
（Ⅲ）如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
体育锻炼与身高达标2×2列联表
| 身高达标 | 身高不达标 | 总计 | |
| 积极参加体育锻炼 | 40 | ||
| 不积极参加体育锻炼 | 15 | ||
| 总计 | 100 |
（ⅱ）请问有多大的把握认为体育锻炼与身高达标有关系？
参考公式：K2=
| π(ac-bd)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P（K2≥k） | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
某学校高三年级有学生1000名，经调查研究，其中750名同学经常参加体育锻炼（称为A类同学），另外250名同学不经常参加体育锻炼（称为B类同学），现用分层抽样方法（按A类、B类分二层）从该年级的学生中共抽查100名同学．
（Ⅰ）求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
（Ⅱ）测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如右图：
（ⅰ）统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170）的中点值为165）作为代表．据此，计算这100名学生身高数据的期望μ及标准差φ（精确到0.1）；
（ⅱ）若总体服从正态分布，以样本估计总体，据此，估计该年级身高在（158.6，181.4）范围中的学生的人数．
（Ⅲ）如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
体育锻炼与身高达标2×2列联表
（ⅰ）完成上表；
（ⅱ）请问有多大的把握认为体育锻炼与身高达标有关系？
参考公式：K2=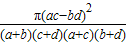
，参考数据：
查看习题详情和答案>>
（Ⅰ）求甲、乙两同学都被抽到的概率，其中甲为A类同学，乙为B类同学；
（Ⅱ）测得该年级所抽查的100名同学身高（单位：厘米）频率分布直方图如右图：
（ⅰ）统计方法中，同一组数据常用该组区间的中点值（例如区间[160，170）的中点值为165）作为代表．据此，计算这100名学生身高数据的期望μ及标准差φ（精确到0.1）；
（ⅱ）若总体服从正态分布，以样本估计总体，据此，估计该年级身高在（158.6，181.4）范围中的学生的人数．
（Ⅲ）如果以身高达170cm作为达标的标准，对抽取的100名学生，得到下列联表：
体育锻炼与身高达标2×2列联表
| 身高达标 | 身高不达标 | 总计 | |
| 积极参加体育锻炼 | 40 | ||
| 不积极参加体育锻炼 | 15 | ||
| 总计 | 100 |
（ⅱ）请问有多大的把握认为体育锻炼与身高达标有关系？
参考公式：K2=
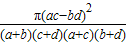，参考数据：| P（K2≥k） | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看习题详情和答案>>