题目内容
给出下列命题：①函数
的最小值为5；②若直线y=kx+1与曲线y=|x|有两个交点，则k的取值范围是-1≤k≤1；
③若直线m被两平行线l1：x-y+1=0与l2：x-y+3=0所截得的线段的长为2
，则m的倾斜角可以是15°或75°④设Sn是公差为d（d≠0）的无穷等差数列{an}的前n项和，若对任意n∈N*，均有Sn＞0，则数列{Sn}是递增数列
⑤设△ABC的内角A．B．C所对的边分别为a，b，c，若三边的长为连续的三个正整数，且A＞B＞C，3b=20acosA则sinA：sinB：sinC为6：5：4
其中所有正确命题的序号是 ．
【答案】分析：①化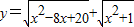
=
=
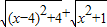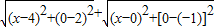，几何意义为x轴上点（x，0）到两定点（4，2），（0，-1）距离．数形结合求出最小值．
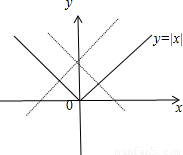
②在同一坐标系内作出y=kx+1与y=|x|的图象，可知当k=±1时，有一个交点．
③先求两平行线间的距离，结合题意直线m被两平行线l1与l2所截得的线段的长为
，求出直线m与l1的夹角为30°，推出结果．
④a1=S1＞0，若d＜0，则数列数列{an}为递减数列，总存在n∈N*，使得Sn＜0，假设不成立．
⑤由题意可得三边即 a、a-1、a-2，由余弦定理可得 cosA=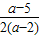
，再由3b=20acosA，可得 cosA=
=
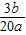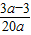，从而可得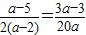
，由此解得a=6，可得三边长，根据sinA：sinB：sinC=a：b：c，求得结果
解答：解：①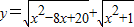
=
=
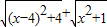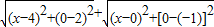
即求x轴上点（x，0）到两定点（4，2），（0，-1）距离和的最小值 而两点位于x轴的两侧，所以最小值即两点的距离最短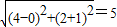
①正确
②在同一坐标系内作出y=kx+1与y=|x|的图象，可知当k=±1时，有一个交点．②错误
③两平行线间的距离为d=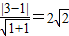
，
由图知直线m与l1的夹角为30°，l1的倾斜角为45°，
所以直线m的倾斜角等于30°+45°=75°或45°-30°=15°．③正确
④若对任意n∈N*，均有Sn＞0，则a1=S1＞0，若d＜0，则数列数列{an}为递减数列，总存在n∈N*，使得Sn＜0，假设不成立，必有d＞0，数列{Sn}是递增数列．④正确．
⑤由于a，b，c 三边的长为连续的三个正整数，且A＞B＞C，可设三边长分别为 a、a-1、a-2．
由余弦定理可得 cosA=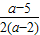
，又3b=20acosA，可得 cosA=
=
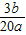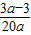
从而可得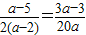
，解得a=6，故三边分别为6，5，4．
由正弦定理可得 sinA：sinB：sinC=a：b：c=a：（a-1）：（ a-2）=6：5：4，⑤正确
综上所述，正确答案序号为①③④⑤
故答案为：①③④⑤
点评：本题以命题真假的判断为载体，着重考查了函数最值，图象与性质，两条直线夹角，数列的单调性，正弦定理、余弦定理的应用．属于中档题．
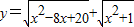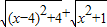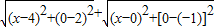==，几何意义为x轴上点（x，0）到两定点（4，2），（0，-1）距离．数形结合求出最小值．②在同一坐标系内作出y=kx+1与y=|x|的图象，可知当k=±1时，有一个交点．
③先求两平行线间的距离，结合题意直线m被两平行线l1与l2所截得的线段的长为
，求出直线m与l1的夹角为30°，推出结果．④a1=S1＞0，若d＜0，则数列数列{an}为递减数列，总存在n∈N*，使得Sn＜0，假设不成立．
⑤由题意可得三边即 a、a-1、a-2，由余弦定理可得 cosA=
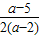，再由3b=20acosA，可得 cosA=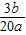=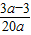，从而可得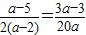，由此解得a=6，可得三边长，根据sinA：sinB：sinC=a：b：c，求得结果解答：解：①
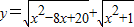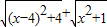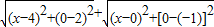
==即求x轴上点（x，0）到两定点（4，2），（0，-1）距离和的最小值 而两点位于x轴的两侧，所以最小值即两点的距离最短
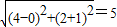①正确②在同一坐标系内作出y=kx+1与y=|x|的图象，可知当k=±1时，有一个交点．②错误
③两平行线间的距离为d=
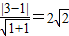，由图知直线m与l1的夹角为30°，l1的倾斜角为45°，
所以直线m的倾斜角等于30°+45°=75°或45°-30°=15°．③正确
④若对任意n∈N*，均有Sn＞0，则a1=S1＞0，若d＜0，则数列数列{an}为递减数列，总存在n∈N*，使得Sn＜0，假设不成立，必有d＞0，数列{Sn}是递增数列．④正确．
⑤由于a，b，c 三边的长为连续的三个正整数，且A＞B＞C，可设三边长分别为 a、a-1、a-2．
由余弦定理可得 cosA=
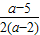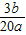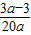
，又3b=20acosA，可得 cosA==从而可得
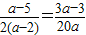，解得a=6，故三边分别为6，5，4．由正弦定理可得 sinA：sinB：sinC=a：b：c=a：（a-1）：（ a-2）=6：5：4，⑤正确
综上所述，正确答案序号为①③④⑤
故答案为：①③④⑤
点评：本题以命题真假的判断为载体，着重考查了函数最值，图象与性质，两条直线夹角，数列的单调性，正弦定理、余弦定理的应用．属于中档题．
练习册系列答案
相关题目