摘要:(Ⅱ)由正弦定理.又.故----8分
网址:http://m.1010jiajiao.com/timu_id_389791[举报]
已知 中,
中, ,
, .设
.设 ,记
,记 .
.
(1) 求 的解析式及定义域;
的解析式及定义域;
(2)设 ,是否存在实数
,是否存在实数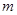 ,使函数
,使函数 的值域为
的值域为 ?若存在,求出
?若存在,求出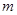 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问利用(1)如图,在 中,由
中,由 ,,
,,
可得 ,
,
又AC=2,故由正弦定理得

(2)中
由 可得
可得

 .显然,
.显然, ,则
,则
1 当m>0的值域为
当m>0的值域为
 m+1=3/2,n=1/2
m+1=3/2,n=1/2
2 当m<0,不满足
当m<0,不满足 的值域为
的值域为 ;
;
因而存在实数m=1/2 的值域为
的值域为 .
.
查看习题详情和答案>>
在△ABC中,内角A、B、C所对边的边长分别是a、b、c,已知c=2,C= .
.
(Ⅰ)若△ABC的面积等于 ,求a、b;
,求a、b;
(Ⅱ)若 ,求△ABC的面积.
,求△ABC的面积.
【解析】第一问中利用余弦定理及已知条件得 又因为△ABC的面积等于
又因为△ABC的面积等于 ,所以
,所以 ,得
,得 联立方程,解方程组得
联立方程,解方程组得 .
.
第二问中。由于 即为即
即为即 .
.
当 时,
时,
 ,
,  ,
,  ,
,
 所以
所以 当
当 时,得
时,得 ,由正弦定理得
,由正弦定理得 ,联立方程组
,联立方程组 ,解得
,解得 ,得到
,得到 。
。
解:(Ⅰ) (Ⅰ)由余弦定理及已知条件得 ,………1分
,………1分
又因为△ABC的面积等于 ,所以
,所以 ,得
,得 ,………1分
,………1分
联立方程,解方程组得 .
……………2分
.
……………2分
(Ⅱ)由题意得
 ,
,
即 .
…………2分
.
…………2分
当 时,
时,
 ,
,  ,
,  ,
,
 ……1分
……1分
所以 ………………1分
………………1分
当 时,得
时,得 ,由正弦定理得
,由正弦定理得 ,联立方程组
,联立方程组
 ,解得
,解得 ,
, ;
所以
;
所以
查看习题详情和答案>>