题目内容
在△ABC中，内角A、B、C所对边的边长分别是a、b、c，已知c=2，C=
.
(Ⅰ)若△ABC的面积等于
，求a、b;
(Ⅱ)若
,求△ABC的面积.
【解析】第一问中利用余弦定理及已知条件得
又因为△ABC的面积等于，所以
，得
联立方程，解方程组得
.
第二问中。由于即为即
.
当
时，
, 
, 
,
所以
当
时，得
，由正弦定理得
，联立方程组，解得
,得到。
解：（Ⅰ） （Ⅰ）由余弦定理及已知条件得，………1分
又因为△ABC的面积等于，所以，得，………1分
联立方程，解方程组得.
……………2分
（Ⅱ）由题意得
，
即.
…………2分
当时，
, , ,
……1分
所以 ………………1分
当时，得，由正弦定理得，联立方程组
，解得,
;
所以
【答案】
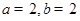（Ⅰ）
. （Ⅱ）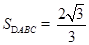
练习册系列答案
相关题目