D 解析:由正弦定理得.又由椭圆定义得AB+BC=2×5＝10.AC=8. 所以题目和参考答案——青夏教育精英家教网—

题目内容

解析：由正弦定理得.又由椭圆定义得AB+BC=2×5＝10.AC=8. 所以

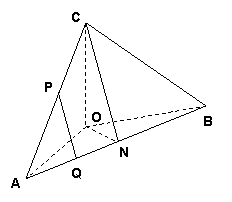
解法一：

（Ⅰ）在平面内作交于，连接。

又，　

，。

取为的中点，则。

在等腰　中，，

在中，，

在中，， .

（Ⅱ）连接，由，知：.

又，

又由，.

是在平面内的射影.

在等腰中，为的中点，

根据三垂线定理，知： ,

为二面角的平面角.

在等腰中，，

在中，，中，.

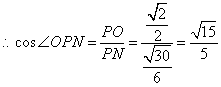
解法二：（Ⅰ）取为坐标原点，分别以，所在的直线为轴，轴，建立空间直角坐标系（如图所示）,则 , 为中点，.

设 .

即，。

所以存在点使得且.

（Ⅱ）记平面的法向量为,则由，，

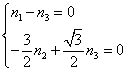且，得，故可取

又平面的法向量为 ..

二面角的平面角是锐角，记为，则.

练习册系列答案

相关题目

如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1.

（Ⅰ）证明PC⊥AD；

（Ⅱ）求二面角A-PC-D的正弦值；

（Ⅲ）设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长.

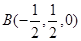【解析】解法一：如图，以点A为原点建立空间直角坐标系，依题意得A(0,0,0)，D(2,0,0),C(0,1,0), ,P（0,0,2）.

（1）证明：易得，于是,所以

(2) ,设平面PCD的法向量，

则,即.不防设，可得.可取平面PAC的法向量于是从而.

所以二面角A-PC-D的正弦值为.

（3）设点E的坐标为（0,0，h），其中，由此得.

由，故

所以，，解得，即.

解法二：（1）证明：由，可得，又由,,故.又,所以.

(2)如图，作于点H，连接DH.由,,可得.

因此,从而为二面角A-PC-D的平面角.在中，,由此得由（1）知,故在中，

因此所以二面角的正弦值为.

（3）如图，因为，故过点B作CD的平行线必与线段AD相交，设交点为F，连接BE，EF. 故或其补角为异面直线BE与CD所成的角.由于BF∥CD，故.在中，故

在中，由,,

可得.由余弦定理，,

所以.

解析：由正弦定理得.又由椭圆定义得AB+BC=2×5＝10.AC=8. 所以

在△ABC中，已知B＝45°,D是BC边上的一点，AD＝10,AC＝14,DC＝6，

求⑴ ∠ADB的大小；⑵ BD的长.

【解析】本试题主要考查了三角形的余弦定理和正弦定理的运用

第一问中，∵cos∠ADC＝

＝＝－∴ cos∠ADB＝cos(180°－∠ADC)＝－cos∠ADC＝∴ cos∠ADB＝60°

第二问中，结合正弦定理∵∠DAB＝180°－∠ADB－∠B＝75°

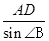由＝得BD＝＝5(＋1)

解：⑴ ∵cos∠ADC＝

＝＝－,……………………………3分

∴ cos∠ADB＝cos(180°－∠ADC)＝－cos∠ADC＝， ……………5分

∴ cos∠ADB＝60° ……………………………6分

⑵ ∵∠DAB＝180°－∠ADB－∠B＝75° ……………………………7分

由＝ ……………………………9分

得BD＝＝5(＋1)

试题分类