摘要:已知线段PA⊥矩形ABCD所在平面.M.N分别是AB.PC的中点.(Ⅰ)求证:MN//平面PAD,(Ⅱ)当∠PDA=45°时.求证:MN⊥平面PCD,
网址:http://m.1010jiajiao.com/timu_id_38314[举报]
(本小题满分12分)已知四棱锥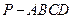 底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F分别是线段AB.BC的中点,
底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F分别是线段AB.BC的中点,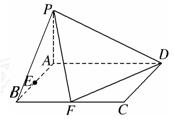
(1)证明:PF⊥FD;
(2)在PA上找一点G,使得EG∥平面PFD;.
(3)若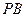 与平面
与平面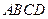 所成的角为
所成的角为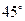 ,求二面角
,求二面角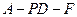 的余弦值.
的余弦值.
(本小题满分12分)
已知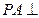 矩形ABCD所在平面,PA=AD=
矩形ABCD所在平面,PA=AD=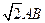 ,E为线段PD上一点。
,E为线段PD上一点。
(1)当E为PD的中点时,求证: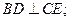
(2)是否存在E使二面角E—AC—D为30°?若存在,求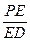 ,若不存在,说明理由。
,若不存在,说明理由。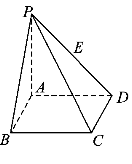
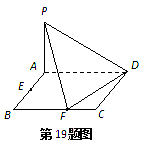 证明:PF⊥FD;
证明:PF⊥FD;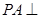 矩形ABCD所在平面,PA=AD=
矩形ABCD所在平面,PA=AD=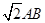 ,E为线段PD上一点。
,E为线段PD上一点。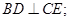
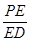 ,若不存在,说明理由。
,若不存在,说明理由。
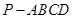 底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F分别是线段AB.BC的中点,
底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F分别是线段AB.BC的中点,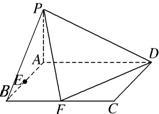
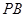 与平面
与平面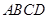 所成的角为
所成的角为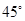 ,求二面角
,求二面角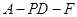 的余弦值.
的余弦值.