Question

（本小题满分12分）

    已知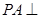矩形ABCD所在平面，PA=AD=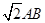，E为线段PD上一点。

    （1）当E为PD的中点时，求证：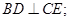

    （2）是否存在E使二面角E—AC—D为30°？若存在，求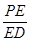，若不存在，说明理由。

 

Answer 1

【答案】

①证明：不妨设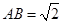，则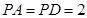，取AD的中点F，连EF，CF。易知∽，∴

∴

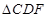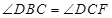
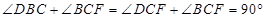
∴BD⊥CF

又EF∥PA，PA⊥平面ABCD

∴EF⊥平面ABCD

故由三垂线定理知BD⊥CE（5分）

②作EG⊥AD于G，过G作GH⊥AC于H，连EH，则可证∠EHG为二面角E-AC-D的平面角。

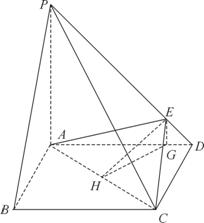
设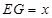，则，

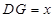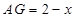∴，又，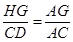

∴，∴，

∴，∴，

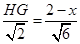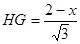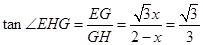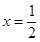所以存在点E满足条件，且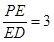（7分）

 

【解析】略