摘要:(Ⅲ)当k为奇数时. 设.数列的前项和为.证明不等式
网址:http://m.1010jiajiao.com/timu_id_371104[举报]












设函数f(x)=2sin(ωx+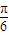 )+k(0<ω<π),将f(x)的图象按
)+k(0<ω<π),将f(x)的图象按 =(
=( ,-1)平移后得一奇函数,
,-1)平移后得一奇函数,
(Ⅰ)求当x∈[0,2]时函数y=f(x)的值域
(Ⅱ)设数列{an}的通项公式为an=f(n)(n∈N+),Sn为其前N项的和,求S2010的值.
查看习题详情和答案>>
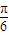 )+k(0<ω<π),将f(x)的图象按
)+k(0<ω<π),将f(x)的图象按 =(
=( ,-1)平移后得一奇函数,
,-1)平移后得一奇函数,(Ⅰ)求当x∈[0,2]时函数y=f(x)的值域
(Ⅱ)设数列{an}的通项公式为an=f(n)(n∈N+),Sn为其前N项的和,求S2010的值.
查看习题详情和答案>>
设函数f(x)=2sin(ωx+ )+k(0<ω<π),将f(x)的图象按
)+k(0<ω<π),将f(x)的图象按 =(
=( ,-1)平移后得一奇函数,
,-1)平移后得一奇函数,
(Ⅰ)求当x∈[0,2]时函数y=f(x)的值域
(Ⅱ)设数列{an}的通项公式为an=f(n)(n∈N+),Sn为其前N项的和,求S2010的值.
查看习题详情和答案>>
设函数f(x)=x2-2(-1)klnx(k∈N*),![]() 表示f(x)导函数.
表示f(x)导函数.
(Ⅰ)求函数一份(x)的单调递增区间;
(Ⅱ)当k为偶数时,数列{an}满足a1=1,![]() .证明:数列{an2}中不存在成等差数列的三项;
.证明:数列{an2}中不存在成等差数列的三项;
(Ⅲ)当k为奇数时,设![]() ,数列{bn}的前n项和为Sn,证明不等式
,数列{bn}的前n项和为Sn,证明不等式![]() 对一切正整数n均成立,并比较S2009-1与ln2009的大小.
对一切正整数n均成立,并比较S2009-1与ln2009的大小.
设函数f(x)=x2-2(-1)klnx(k∈N*),![]() (x)表示f(x)导函数.
(x)表示f(x)导函数.
(Ⅰ)求函数一份(x)的单调递增区间;
(Ⅱ)当k为偶数时,数列{an}满足a1=1,an![]() (an)=
(an)=![]() -3.证明:数列{
-3.证明:数列{![]() }中不存在成等差数列的三项;
}中不存在成等差数列的三项;
(Ⅲ)当k为奇数时,设bn=![]() (n)-n,数列{bn}的前n项和为Sn,证明不等式
(n)-n,数列{bn}的前n项和为Sn,证明不等式![]() 对一切正整数n均成立,并比较S2009-1与In2009的大小.
对一切正整数n均成立,并比较S2009-1与In2009的大小.
 已知数列{an}的前n项和为Sn,a1=1,a4=8,Sn=b•qn+c(q≠0,q≠±1,bc≠0,b+c=0),现把数列{an}的各项排成如图所示的三角形形状.记A(m,n)为第m行从左起第n个数(m、n∈N*).有下列命题:
已知数列{an}的前n项和为Sn,a1=1,a4=8,Sn=b•qn+c(q≠0,q≠±1,bc≠0,b+c=0),现把数列{an}的各项排成如图所示的三角形形状.记A(m,n)为第m行从左起第n个数(m、n∈N*).有下列命题:①{an}为等比数列且其公比q=±2;
②当n=2m(m>3)时,A(m,n)不存在;
③a28=A(6,9),A(11,1)=2100;
④假设m为大于5的常数,且A(m,1)=am1,A(m,2)=am2…A(m,k)=amk,其中amk为A(m,n)的最大值,从所有m1,m2,m3,…,mk中任取一个数,若取得的数恰好为奇数的概率为
| m-1 | 2m-1 |
其中你认为正确的所有命题的序号是
②③④
②③④
.