题目内容
设函数f(x)=2sin(ωx+ )+k(0<ω<π),将f(x)的图象按
)+k(0<ω<π),将f(x)的图象按 =(
=( ,-1)平移后得一奇函数,
,-1)平移后得一奇函数,
(Ⅰ)求当x∈[0,2]时函数y=f(x)的值域
(Ⅱ)设数列{an}的通项公式为an=f(n)(n∈N+),Sn为其前N项的和,求S2010的值.
解:(Ⅰ)由题意,设函数f(x)=2sin(ωx+ )+k(0<ω<π),将f(x)的图象按
)+k(0<ω<π),将f(x)的图象按 =(
=( ,-1)平移后,得到函数g(x),则
,-1)平移后,得到函数g(x),则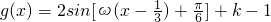
∵g(x)为奇函数
∴所以k=1,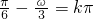 ,∴
,∴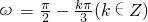
∵0<ω<π,∴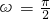
∴f(x)=2sin( x+
x+ )+1┅┅┅┅┅(3分)
)+1┅┅┅┅┅(3分)
∵x∈[0,2],∴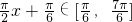
∴sin( x+
x+ )
)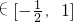
∴f(x)∈[0,3]┅┅┅┅┅┅┅┅┅┅(6分)
(Ⅱ)∵an=f(n),∴an=2sin( n+
n+ )+1,T=4
)+1,T=4
∴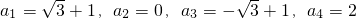 ┅┅┅┅┅┅┅┅(8分)
┅┅┅┅┅┅┅┅(8分)
∴S2010=502(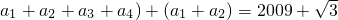 +a1+a2=2009+
+a1+a2=2009+ ┅┅┅(12分)
┅┅┅(12分)
分析:(Ⅰ)根据将f(x)的图象按 =(
=( ,-1)平移,可得到平移后的函数
,-1)平移,可得到平移后的函数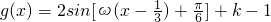 ,利用g(x)为奇函数,可得k=1,
,利用g(x)为奇函数,可得k=1,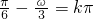 ,结合0<ω<π,即可求得函数f(x)的解析式,进而整体思维,由x∈[0,2],确定
,结合0<ω<π,即可求得函数f(x)的解析式,进而整体思维,由x∈[0,2],确定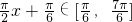 ,从而可求当x∈[0,2]时函数y=f(x)的值域;
,从而可求当x∈[0,2]时函数y=f(x)的值域;
(Ⅱ)由an=f(n),可得an=2sin( n+
n+ )+1,数列的周期为4,根据S2010=502(
)+1,数列的周期为4,根据S2010=502(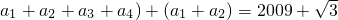 +a1+a2,可得结论.
+a1+a2,可得结论.
点评:本题以向量的平移为载体,考查数列与三角函数的结合,考查三角函数的性质,同时考查了三角函数的值域,综合性强.
 )+k(0<ω<π),将f(x)的图象按
)+k(0<ω<π),将f(x)的图象按 =(
=( ,-1)平移后,得到函数g(x),则
,-1)平移后,得到函数g(x),则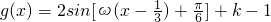
∵g(x)为奇函数
∴所以k=1,
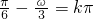 ,∴
,∴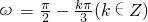
∵0<ω<π,∴
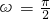
∴f(x)=2sin(
 x+
x+ )+1┅┅┅┅┅(3分)
)+1┅┅┅┅┅(3分)∵x∈[0,2],∴
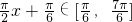
∴sin(
 x+
x+ )
)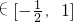
∴f(x)∈[0,3]┅┅┅┅┅┅┅┅┅┅(6分)
(Ⅱ)∵an=f(n),∴an=2sin(
 n+
n+ )+1,T=4
)+1,T=4∴
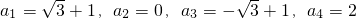 ┅┅┅┅┅┅┅┅(8分)
┅┅┅┅┅┅┅┅(8分)∴S2010=502(
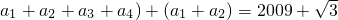 +a1+a2=2009+
+a1+a2=2009+ ┅┅┅(12分)
┅┅┅(12分)分析:(Ⅰ)根据将f(x)的图象按
 =(
=( ,-1)平移,可得到平移后的函数
,-1)平移,可得到平移后的函数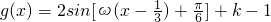 ,利用g(x)为奇函数,可得k=1,
,利用g(x)为奇函数,可得k=1,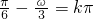 ,结合0<ω<π,即可求得函数f(x)的解析式,进而整体思维,由x∈[0,2],确定
,结合0<ω<π,即可求得函数f(x)的解析式,进而整体思维,由x∈[0,2],确定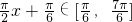 ,从而可求当x∈[0,2]时函数y=f(x)的值域;
,从而可求当x∈[0,2]时函数y=f(x)的值域;(Ⅱ)由an=f(n),可得an=2sin(
 n+
n+ )+1,数列的周期为4,根据S2010=502(
)+1,数列的周期为4,根据S2010=502(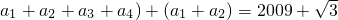 +a1+a2,可得结论.
+a1+a2,可得结论.点评:本题以向量的平移为载体,考查数列与三角函数的结合,考查三角函数的性质,同时考查了三角函数的值域,综合性强.

练习册系列答案
相关题目