网址:http://m.1010jiajiao.com/timu_id_36946[举报]
说明:
一、本解答给出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则。
二、对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定后续部分的给分,但不得超过该部分正确解答所给分数的一半;如果后续部分的解答存在较严重的错误,则不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。
四、每题只给整数分数,选择题和填空题不给中间分。
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
C
D
A
A
B
C
B
D
二、填空题:
11.40.6,1.1 12. 13.
13. 14.30 15.
14.30 15.  16.(1,1),(2,2),(3,4),(4,8)
16.(1,1),(2,2),(3,4),(4,8)
三、解答题:
17.(Ⅰ) , ①
…………………2分
, ①
…………………2分
又 , ∴
, ∴ ②
……………… 4分
②
……………… 4分
由①、②得 …………………………………………………………… 6分
…………………………………………………………… 6分
(Ⅱ)
 ……………………………………… 8分
……………………………………… 8分
 …………………………………………………………………… 10分
…………………………………………………………………… 10分

 …………………………………………………………………………12分
…………………………………………………………………………12分
18.(Ⅰ)设点
 ,则
,则 ,
,
 ,
,
 ,又
,又 ,
,
 ,∴椭圆的方程为:
,∴椭圆的方程为: …………………………………………7分
…………………………………………7分
(Ⅱ)当过 直线
直线 的斜率不存在时,点
的斜率不存在时,点 ,则
,则 ;
;
当过 直线
直线 的斜率存在时,设斜率为
的斜率存在时,设斜率为 ,则直线
,则直线 的方程为
的方程为 ,
,
设 ,由
,由 得:
得:
 …………………………………………10分
…………………………………………10分

 ……13分
……13分
综合以上情形,得: ……………………………………………………14分
……………………………………………………14分
|

 面EFG,PB
面EFG,PB 平面EFG,
平面EFG, ,
, ,又GM=
,又GM= ,………………7分
,………………7分 ………………8分
………………8分 ,
………………………………9分
,
………………………………9分
 ,则
,则
 ,
…………………………13分
,
…………………………13分 故存在点Q,当CQ=
故存在点Q,当CQ= 时,点A到平面EFQ的距离为0.8. ……………………… 14分
时,点A到平面EFQ的距离为0.8. ……………………… 14分

 …………1分
…………1分 , 即
, 即 ,
,
 ……………3分
……………3分 ,∴PB∥平面EFG. ………………………………………………………… 4分
,∴PB∥平面EFG. ………………………………………………………… 4分 ,
…………………………………………5分
,
…………………………………………5分 ,
……………………… 8分
,
……………………… 8分
 ……………………………………10分
……………………………………10分 , 设平面EFQ的法向量为
, 设平面EFQ的法向量为 ,则
,则

 , ……………………………………………………12分
, ……………………………………………………12分 , ∴点A到平面EFQ的距离
, ∴点A到平面EFQ的距离 ,……13分
,……13分 ,
, 不合题意,舍去.
不合题意,舍去. ,
, ………………2分
………………2分 时,
时, , …………4分
, …………4分
 是单调增函数; ………………6分
是单调增函数; ………………6分
 是单调减函数; ………………8分
是单调减函数; ………………8分 是偶函数,对任意
是偶函数,对任意 都有
都有 成立
成立 对任意
对任意 或
或 时,
时, 是定义域上的单调函数,
是定义域上的单调函数,
 时,对任意
时,对任意 时,
时, ,由
,由
 上是单调增函数
上是单调增函数 在上是单调减函数,∴对任意
在上是单调减函数,∴对任意

 时,对任意
时,对任意 时,对任意
时,对任意 }的公差是
}的公差是 ,则
,则 ,解得
,解得
 ……………………………………2分
……………………………………2分 =-1<0
=-1<0 适合条件①;又
适合条件①;又 ,所以当
,所以当 =4或5时,
=4或5时, 取得最大值20,即
取得最大值20,即 …………………………………………4分
…………………………………………4分 ,所以当n≥3时,
,所以当n≥3时, ,此时数列
,此时数列 单调递减;当
单调递减;当 ,即
,即
 ,所以
,所以 ≥7………………………………………………………8分
≥7………………………………………………………8分 成立,
成立, 的各项均为正整数,可得
的各项均为正整数,可得 ……………10分
……………10分 ……11分
……11分 …13分
…13分
 ……………………………………………15分
……………………………………………15分 ,总有
,总有 ,故有
,故有 ,这与数列(
,这与数列( )的各项均为正整数矛盾!
)的各项均为正整数矛盾! ,都有
,都有 成立. ………………………16分
成立. ………………………16分


 ,求△AOB面积的最大值
,求△AOB面积的最大值 的方程;
的方程; 在
在 轴上截距的取值范围;
轴上截距的取值范围; 面积的最大值
面积的最大值 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合. 的值.
的值. 交椭圆
交椭圆 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合. 的值.
的值. 交椭圆
交椭圆 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆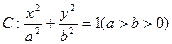
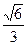
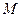
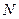
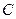
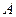
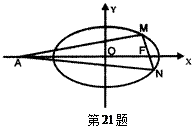 (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程;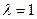 时,
时,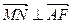 ;
;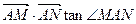 =6
=6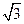 时, 求直线MN的方程
时, 求直线MN的方程