网址:http://m.1010jiajiao.com/timu_id_358894[举报]
一、填空题(本大题满分60分,共12小题,每小题满分5分)
10. 6 11.①⑤ 12. 2
二、选择题(本大题满分16分,共4小题,每小题满分4分)
三、解答题(本大题满分74,共5小题)
17.解:(1)取BC的中点F,连接EF、AF,则EF//PB,
所以∠AEF就是异面直线AE和PB所成角或其补角;
……………3分
∵∠BAC=60°,PA=AB=AC=2,PA⊥平面ABC,
(2)因为E是PC中点,所以E到平面ABC的距离为.files/image114.gif) …………10分
…………10分
18.(本题满分14分)
19.(本题满分14分)
20.(本题满分16分,第1小题满分6分,第2小题满分10分)
雪花曲线的特性是周长无限增大而面积有限的图形。 ………………16分
(第3小题酌情给分)
21.(本题20分,第1小题满分4分,第2小题满分6分,第3小题6分,第4小题4分)
消去
.files/image170.gif) 的距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与椭圆相交的充要条件为:
的距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与椭圆相交的充要条件为:.files/image172.gif) ;直线L与椭圆M相切的充要条件为:
;直线L与椭圆M相切的充要条件为:.files/image174.gif) ;直线L与椭圆M相离的充要条件为:
;直线L与椭圆M相离的充要条件为:.files/image176.gif) ……14分
……14分
命题得证。
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
(4)可以类比到双曲线:设F1、F2是双曲线.files/image182.gif) 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线.files/image183.gif) 距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为:
距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为:.files/image172.gif) ;直线L与双曲线M相切的充要条件为:
;直线L与双曲线M相切的充要条件为:.files/image174.gif) ;直线L与双曲线M相离的充要条件为:
;直线L与双曲线M相离的充要条件为:.files/image176.gif)
………………20分
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
本资料由《七彩教育网》www.7caiedu.cn 提供!
(本小题满分12分)
椭圆G: 的左、右焦点分别为
的左、右焦点分别为 ,M是椭圆上的一点,且满足
,M是椭圆上的一点,且满足 =0.
=0.
(1)求离心率e的取值范围;
(1)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为5 .
.
①求此时椭圆G的方程;
②设斜率为 的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,
的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,
问:A、B两点能否关于过点 、Q的直线对称?若能,求出k的取值范
、Q的直线对称?若能,求出k的取值范
围;若不能,请说明理由.
查看习题详情和答案>>
(本小题满分12分)
椭圆G:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,M是椭圆上的一点,且满足
,M是椭圆上的一点,且满足![]() =0.
=0.
(1)求离心率e的取值范围;
(1)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为5![]() .
.
①求此时椭圆G的方程;
②设斜率为![]() 的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,
的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,
问:A、B两点能否关于过点![]() 、Q的直线对称?若能,求出k的取值范
、Q的直线对称?若能,求出k的取值范
围;若不能,请说明理由.
查看习题详情和答案>>| d2 |
| d1 |
| ||
| 2 |
(1)求动点P所在曲线C的方程;
(2)直线l过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线l1:x=-2的垂线,对应的垂足分别为M、N,试判断点F与以线段MN为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)记S1=S△FAM,S2=S△FMN,S3=S△FBN(A、B、M、N是(2)中的点),问是否存在实数λ,使S22=λS1S3成立.若存在,求出λ的值;若不存在,请说明理由.
进一步思考问题:若上述问题中直线l1:x=-
| a2 |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
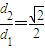 .
.(1)求动点P所在曲线C的方程;
(2)直线l过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线l1:x=-2的垂线,对应的垂足分别为M、N,试判断点F与以线段MN为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)记S1=S△FAM,S2=S△FMN,S3=S△FBN(A、B、M、N是(2)中的点),问是否存在实数λ,使S22=λS1S3成立.若存在,求出λ的值;若不存在,请说明理由.
进一步思考问题:若上述问题中直线
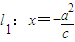 、点F(-c,0)、曲线C:
、点F(-c,0)、曲线C: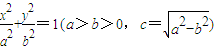 ,则使等式S22=λS1S3成立的λ的值仍保持不变.请给出你的判断______ (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).
,则使等式S22=λS1S3成立的λ的值仍保持不变.请给出你的判断______ (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).查看习题详情和答案>>
.files/image100.gif)
.files/image102.gif)
.files/image104.gif)
.files/image106.gif)
.files/image108.gif)
.files/image110.gif)
.files/image112.gif)
.files/image116.gif)
.files/image118.gif)
.files/image120.gif)
.files/image122.gif)
.files/image124.gif)
.files/image126.gif)
.files/image128.gif)
.files/image130.gif)
.files/image132.gif)
.files/image134.gif)
.files/image136.gif)
.files/image138.gif)
.files/image140.gif)
.files/image142.gif)
.files/image144.gif)
.files/image146.gif)
.files/image148.gif)
.files/image150.gif)
.files/image090.gif)
.files/image152.gif)
.files/image154.gif)
.files/image156.gif)
.files/image158.gif)
.files/image160.gif)
.files/image162.gif)
.files/image164.gif)
.files/image166.gif)
.files/image168.gif)
.files/image178.gif)
.files/image180.gif)
 )及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为
)及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为 、
、 且
且
 与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线
与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线 的距离。(O为坐标原点)
的距离。(O为坐标原点)