Question

已知平面上动点P（）及两个定点A（-2，0），B（2，0），直线PA、PB的斜率分别为、 且

（I）求动点P所在曲线C的方程。

（II）设直线与曲线C交于不同的两点M、N，当OM⊥ON时，求点O到直线的距离。（O为坐标原点）

 

Answer 1

【答案】

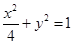（1）    (2)

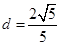
【解析】

试题分析：解：（1）设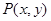由已知得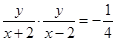 

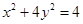
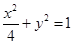
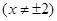     P点的轨迹为一椭圆除去长轴的两端点

（2）设M

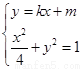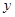 消去得：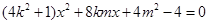

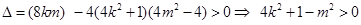
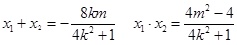
OM⊥ON    ∴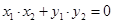

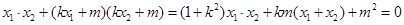
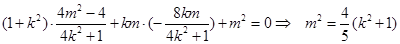
满足

O点到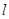的距离为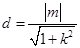 

      

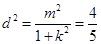
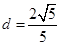
考点：直线与椭圆的位置关系

点评：主要是考查了椭圆方程以及直线与椭圆位置关系的运用，属于中档题。